Análisis descriptivo univariado
0. Objetivo del práctico
El objetivo del práctico es avanzar en el análisis de los datos a través del uso de estadísticos descriptivos. Para esto ya debemos contar con datos previamente procesados del práctico N°6. Previo a eso, siempre es importante que recordemos en qué parte del proceso estamos

En este práctico veremos tanto la estimación puntual de estadísticos descriptivos, como su visualización para reportes, ya sea a través de tablas o de gráficos.
Recursos del práctico
En este práctico utilizamos los datos procesados CASEN 2020, que proviene de los datos originales de la Encuesta de Caracterización Socioeconómica (CASEN). Recuerden siempre consultar el libro códigos antes de trabajar datos.
1. Paquetes a utilizar
Para este práctico utilizaremos, principalmente, las librerías sjmisc y sjPlot.
sjmisc: esta paquete tiene múltiples funciones, desde la transformación de datos y variables. Este paquete suele complementar a dplyr de tidyverse en sus funciones.
sjPlot: su principal función es la visualización de datos para estadística en ciencias sociales mediante tablas y gráficos.
Cargaremos los paquetes con pacman, si aún tienes dudas sobre cómo trabajar con pacman puedes revisar el práctico 2
pacman::p_load(sjmisc,
sjPlot,
tidyverse,
magrittr)
2. Importar datos
Una vez cargados los paquetes a utilizar, debemos continuar cargar los datos. Como indicamos al inicio, seguiremos utilizando los datos CASEN que fueron procesados en el práctico anterior, pero incorporando una nueva variable.
datos_proc <- readRDS("input/data/datos_proc.rds")
3. Explorar datos
Pero ¿cómo sabremos cuales son las nuevas variables que componen la base de datos procesada?, ¡Simple! usaremos dos códigos que vimos en el práctico 4 para conocer los datos procesados que usaremos en esta ocasión:
Primero, usaremos el código names, que nos entrega los nombres de las variables que componen los datos
names(datos_proc)
## [1] "folio" "sexo" "edad" "ocupacion"
## [5] "ytoth" "tot_per" "ife" "o2"
## [9] "o3" "o4" "o6" "ife_d"
## [13] "sexo_edad_tramo" "ing_pc"
Mientras que la función head nos entrega el nombre y las primeras 10 filas que lo componen.
head(datos_proc)
## # A tibble: 6 x 14
## folio sexo edad ocupacion ytoth tot_per ife o2 o3 o4 o6
## <dbl> <fct> <dbl> <fct> <dbl> <dbl> <fct> <fct> <fct> <fct> <fct>
## 1 1.10e11 Masc~ 20 No 3.00e6 3 No No No No No
## 2 1.10e11 Feme~ 56 No 3.00e6 3 No No No Sí No
## 3 1.10e11 Masc~ 77 No 6.10e5 2 No No No Sí No
## 4 1.10e11 Feme~ 60 No 6.10e5 2 No No No Sí No
## 5 1.10e11 Masc~ 18 No 1.32e6 4 Sí No No No No
## 6 1.10e11 Masc~ 82 No 1.11e6 4 No No No Sí No
## # ... with 3 more variables: ife_d <dbl>, sexo_edad_tramo <chr>, ing_pc <dbl>
Estos códigos nos permiten establecer una aproximación a los datos con los cuales trabajaremos, como los posibles valores que pueden adoptar, el tipo de dato para cada variable, entre otros. No obstante, por prácticos anteriores sabemos que podemos explorar nuestros datos con sjPlot::view_df()
sjPlot::view_df(datos_proc,
encoding = "UTF-8")
| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | folio | Identificación hogar (comuna area seg viv hogar) | range: NA-NA | |
| 2 | sexo | Masculino Femenino |
||
| 3 | edad | Edad | range: 15-110 | |
| 4 | ocupacion | o1. La semana pasada, ¿trabajó al menos una hora? | Sà No |
|
| 5 | ytoth | Ingreso total del hogar | range: 0-92666667 | |
| 6 | tot_per | Total de personas en el hogar | range: 1-6 | |
| 7 | ife | y26d_hog. Últimos 12 meses, ¿alguien recibió Ingreso Familiar de Emergencia? |
SÃ No No sabe |
|
| 8 | o2 | o2. Aunque no trabajó la semana pasada, ¿realizó alguna actividad? |
SÃ No |
|
| 9 | o3 | o3. Aunque no trabajó, ¿tenÃa algún empleo del cual estuvo ausente temporalmente |
SÃ No |
|
| 10 | o4 | o4. ¿Ha trabajado alguna vez? | Sà No |
|
| 11 | o6 | o6. ¿Buscó trabajo remunerado o cuenta propia en las últimas cuatro semanas? |
SÃ No |
|
| 12 | ife_d | range: 0-0 | ||
| 13 | sexo_edad_tramo | <output omitted> | ||
| 14 | ing_pc | range: 0.0-18533333.4 | ||
4. Descripción de variables
Una vez conocidas las variables que incluye nuestros datos procesados ¿cómo podemos realizar un análisis descriptivo univariado para algún informe o reporte? Veamos algunas de las más comunes
4.1. Medidas de tendencia central
Para conocer las medidas de tendencia central de las variables hay dos opciones. Por una parte, podemos calcular un estadístico directamente a través de código, obteniendo el valor directamente en la consola (o en nuestro .Rmd, si hemos configurado adecuadamente el chunk respectivo). Por otra, podemos generar un código que presente directamente una tabla resumen de los datos.
Media
Para conocer la media de una variable se utiliza la función mean(), cuya estructura es:
mean(datos$variable, na.rm=TRUE)
El argumento na.rm=TRUE excluye del cálculo a los casos perdidos. Si deséaramos estimar la media de ing_pc, debemos codificar lo siguiente
mean(datos_proc$ing_pc, na.rm=TRUE)
## [1] 270487.2
Media recortada
Pero, ¿qué pasa si, dada la distribución de los valores de la variable ing_pc, su media se ve fuertemente afectadas por casos atípicos o fuera de rango (por ejemplo, que esta adopte un valor más alto producto de una alta concentración de ingresos)? En tal caso, una buena manera de evitar el efecto de casos influyentes en la estimación pasa por calcular la media recortada, incorporando el argumento trim para excluir al 5% de la muestra en la estimación (es decir, el 2.5% de cada extremo)
mean(datos_proc$ing_pc, na.rm=TRUE, trim = 0.025)
## [1] 240518
¿Ven cómo se modifica el valor que obtenemos a partir de esta estimación? La diferencia entre la media y la media recortada al 5% de los ingresos per cápita es de 2.9969194\times 10^{4}.
Una vez conocemos el valor medio de la variable ing_pc, podemos tener una idea más clara de cómo se caracterizan los ingresos per cápita del país a nivel general entre quienes fueron encuestada/os en CASEN. Sin embargo, hay otros estadísticos que nos permitirán generar una representación más clara de los ingresos de los hogares chilenos ¡vamos a estimar la mediana!
Mediana
¿Cuál es el ingreso per cápita máximo al que puede acceder el 50% de los hogares chilenos en el momento en que se recolectaron los datos de CASEN 2020? Para el cálculo de la mediana se utiliza la función median(), que presenta una estructura similar a la de mean():
median(datos$variable, na.rm =TRUE)
median(datos_proc$ing_pc, na.rm =TRUE)
## [1] 197508
Ahora ya sabemos que un 50% de los hogares en Chile tiene un ingreso per cápita de 1.97508\times 10^{5} o menos.
Ya tenemos los estadísticos principales, pero ¿cómo los reportamos? ¿debemos estimar la media y la mediana de cada todas nuestras variables una por una? ¡No!, para ello sjmisc tiene diferentes funciones que nos permitirán estimar y presentar gráficamente tales estimaciones, y las conoceremos a continuación:
Un resumen
Por ello ocuparemos la función descr() de sjmisc, que nos presenta un resumen de los estadísticos básicos, incluyendo las etiquetas de cada variable.
sjmisc::descr(datos_proc$ing_pc,
show = "all",
out = "viewer",
encoding = "UTF-8",
file = "output/figures/tabla-ingreso.doc")
##
## ## Basic descriptive statistics
##
## var type label n NA.prc mean sd se md trimmed
## dd numeric dd 76935 0 270487.2 339959.2 1225.65 197508 218746.6
## range iqr skew
## 18533333.4 (0-18533333.4) 194679.3 13.49
¡Atención! utilizaremos la función descr() sólo para variables de clase numeric ¿Qué sentido tiene calcular el promedio de equipos de futbol, o de religiones que existen?
Como ya adelantamos anteriorme, sjmisc dialoga con el universo tidyverse, por lo cual es posible complementar con funciones como select() de dplyr, seleccionando más de una variable a la vez para nuestras estimaciones de estadísticos de resumen. Además, el argumento file = nos permite exportar la tabla de estadísticos que acabamos de generar en formato .doc (¡y otros!).
datos_proc %>%
select(ing_pc, ytoth, tot_per) %>%
sjmisc::descr(
show = "all",
out = "viewer",
encoding = "UTF-8",
file = "output/figures/tabla1.doc")
##
## ## Basic descriptive statistics
##
## var type label n NA.prc mean
## ing_pc numeric ing_pc 76935 0 270487.24
## ytoth numeric Ingreso total del hogar 76935 0 841208.14
## tot_per numeric Total de personas en el hogar 76935 0 3.32
## sd se md trimmed range iqr skew
## 339959.20 1225.65 197508 218746.62 18533333.4 (0-18533333.4) 194679.3 13.49
## 1205921.22 4347.67 600000 664578.15 92666667 (0-92666667) 606322.0 23.32
## 1.33 0.00 3 3.28 5 (1-6) 2.0 0.21
Como podemos ver, descr() nos presenta diversa información, como el nombre de la variable en var; su tipo en type; su etiqueta en label; los casos válidos en n; el porcentaje de casos perdidos en NA.prc; y las diversas medidas de tendencia central, posición de dispersión para cada una de nuestra variables, como la media y la mediana, los cuartiles, la desviación estándar, y muchas otras.
4.3. Frecuencias
Frecuencias absolutas
Podemos utilizar la función table() del paquete base de R, que presenta la frecuencia absoluta de cada un de los valores que puede alcanzar alguna de nuestras variables categóricas.
table(datos_proc$sexo)
##
## Masculino Femenino
## 28416 48519
También podemos emplear la función flat_table(), que permite agrupar la frecuencia absoluta de las categorías de dos o más de nuestras variables categóricas.
flat_table(datos_proc, sexo, ocupacion, ife)
## ife Sí No No sabe
## sexo ocupacion
## Masculino Sí 0 0 0
## No 10323 17640 453
## Femenino Sí 0 0 0
## No 18702 29032 785
No obstante, el output de ambas funciones no se resulta visualmente atractivo ¿cómo podríamos reportar las frecuencias absolutas (y relativas) en nuestros informes? Si queremos una tabla general usaremos la función frq() de sjmisc, cuyo output es una tabla de frecuencia que presenta. Esta función devuelve una tabla de frecuencias absolutas y relativas para nuestras variables categóricas (¡genial!). Además, si nuestros datos son números etiquetados (dbl + lbl), presenta tanto los valores numéricos como las etiquetas asociadas a cada uno de ellos (¡table() sólo presenta los valores numéricos! no incluye metadata en su output)
sjmisc::frq(datos_proc$sexo,
out = "viewer",
title = "Frecuencias",
encoding = "UTF-8",
file = "output/figures/tabla2.doc")
5. Visualización
Ahora que ya sabemos cómo obtener todos los estadísticos necesarios para escribir nuestros reportes, viene el segundo paso: visualizar tales estadísticos. ¡Siempre es mejor presentar un buen gráfico, antes de mostrar un número y ya! Para ello, emplearemos la librería sjPlot
Para visualizar las frecuencias usaremos la función plot_frq, que se estructura de la siguiente manera
plot_frq(datos, #base
..., #variable
title = "", # título
type = c("bar", "dot", "histogram", "line", "density", "boxplot", "violin") #tipo de gráfico a especificar
Para los gráficos, tenemos los siguientes códigos
- Gráfico de barras de frecuencias simple
Si quisiéramos presentar gráficos que entreguen la frecuencia de cada categoría de respuesta, podemos presentarla de la siguiente forma:
plot_frq(datos_proc, sexo,
title = "Gráfico de frecuencias, barras",
type = "bar")
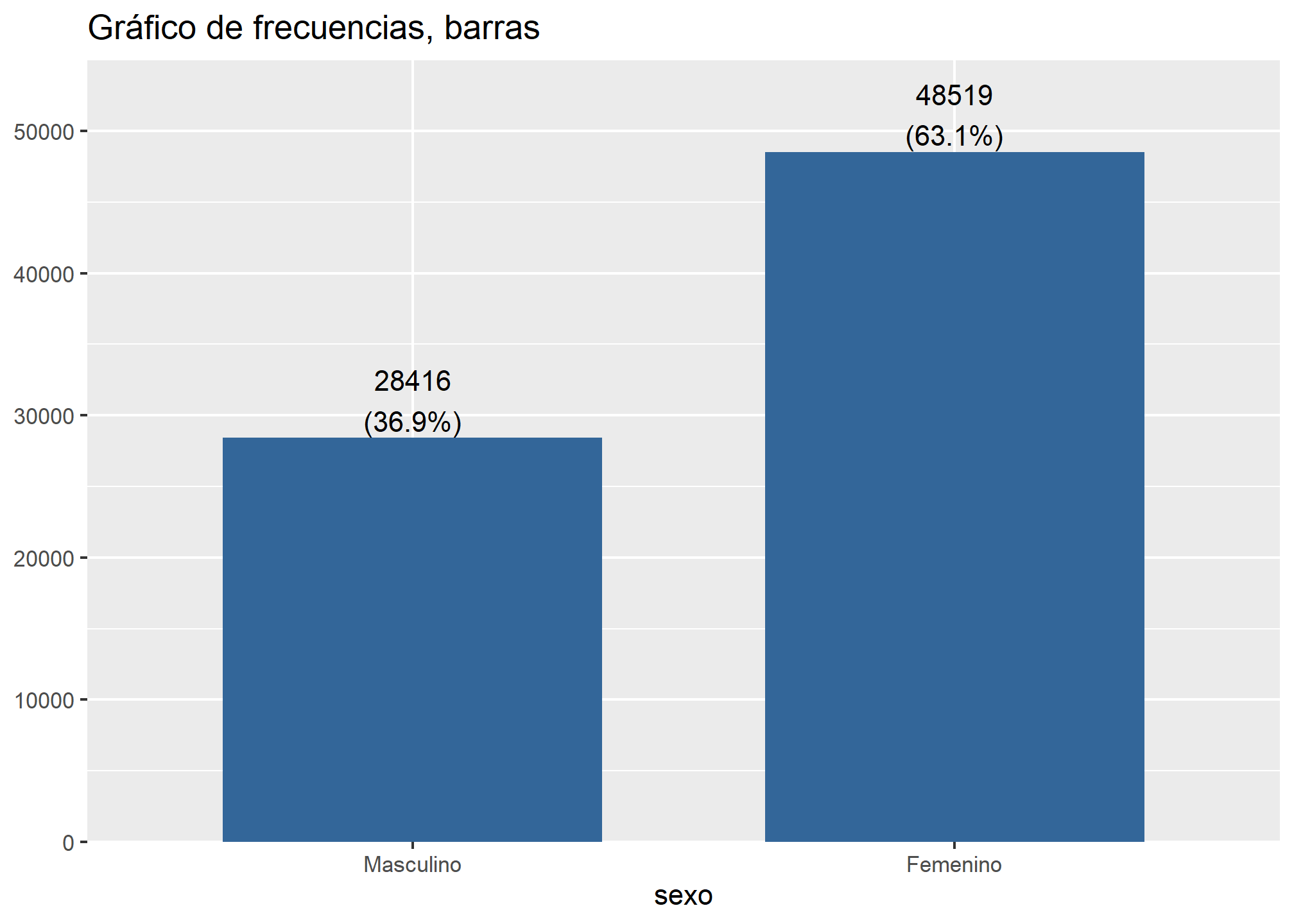
Además de la visualización es importante el guardar los datos que se producen y sjPlot tiene su propio código para hacerlo a través de la función save_plot(), su estructura es esta:
save_plot("ruta/imagen.jpg", fig = last_plot()) #se deja el formato del archivo (.png, .jpg, .svg o .tif) y la ruta de la carpeta
Así guardaríamos el gráfico anterior
save_plot("output/figures/tab.png", fig = last_plot())
- Gráfico de puntos
¡Podemos presentar un gráfico de puntos!
plot_frq(datos_proc, sexo,
title = "Gráfico de frecuencias, puntos",
type = "dot")

También podemos cambiar el orden de los ejes x e y
plot_frq(datos_proc$sexo_edad_tramo, type = "dot", show.ci = TRUE, sort.frq = "desc",
coord.flip = TRUE, expand.grid = TRUE, vjust = "bottom", hjust = "left", title = "Gráfico de frecuencias, puntos cambiado"
)
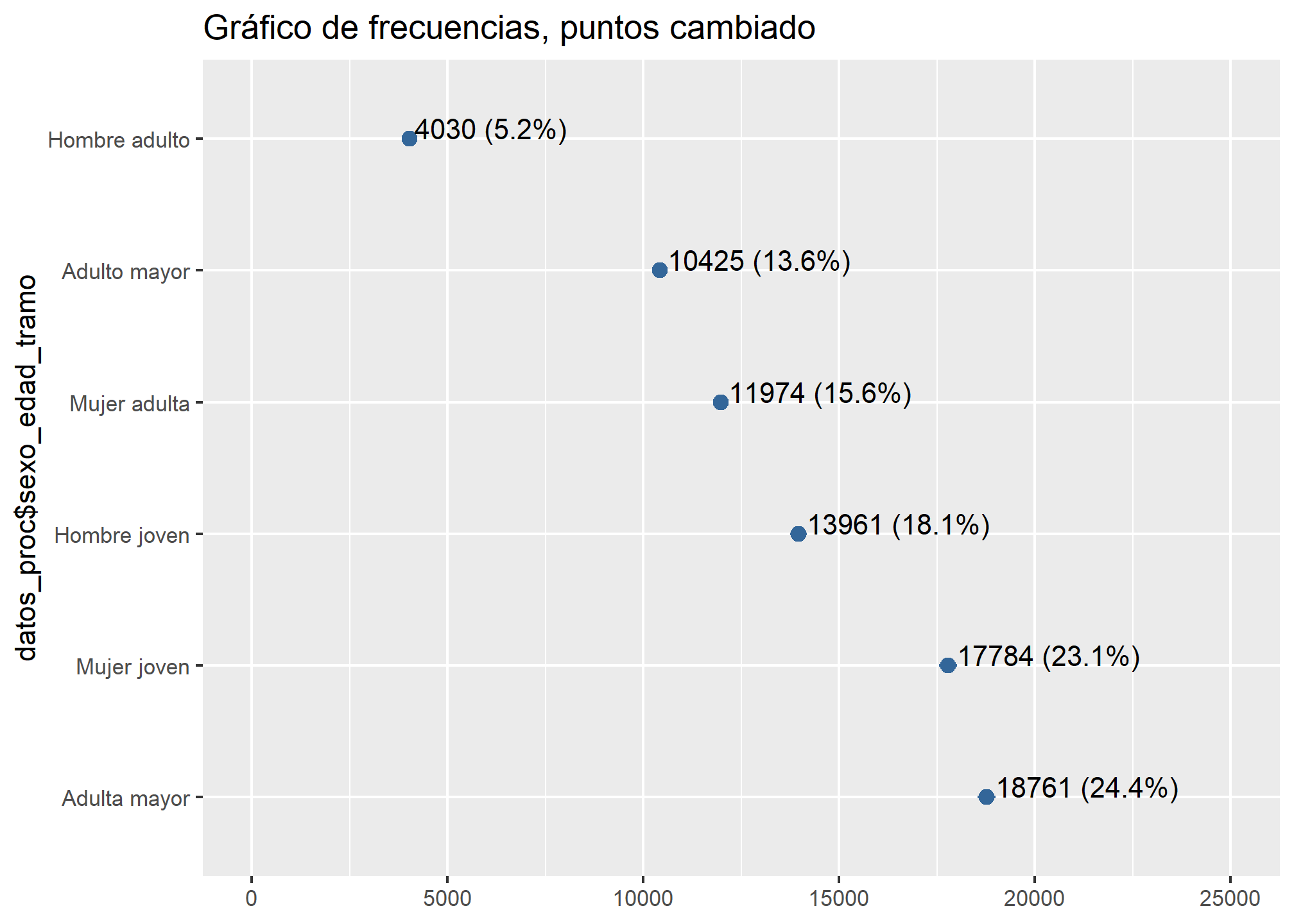
Pero, ¿cuál es el argumento que hace esto?
A la hora de trabajar en R, siempre debemos conocer los argumentos que utilizamos en nuestros códigos, puede que un argumento sea innecesario o esté generando un error, para eso debemos consultar en la sección Help. Los pasos son los siguientes:
a. Escribe en la consola anteponiendo un ? en la función que quieres conocer, en este caso será plot_frq?, quedando así:

b. Una vez le des a Enter, en la sección Help aparecerá información sobre la función, cómo se usa y qué se puede hacer con ella. En Arguments explicará la función de cada argumento

¡Ahora podrán definir, con completo conocimiento, cómo están personalizando sus gráficos!
- Histogramas
Otra función que podemos hacer es graficar histogramas. Sin embargo, como ya hemos visto, la variable ing_pc tiene casos fuera de rango que distorsionan la imagen que nos podemos hacer de la distribución de la variable en la muestra. Para solucionar esto, ocuparemos lo aprendido en el práctico anterior y filtraremos la variable, eliminando de la presentación los ingresos mayores a $2.000.000, con la función filter de dplyr
datos_proc %>% filter(ing_pc <= 2000000) %>%
plot_frq(., ing_pc,
title = "Histograma",
type = "histogram")
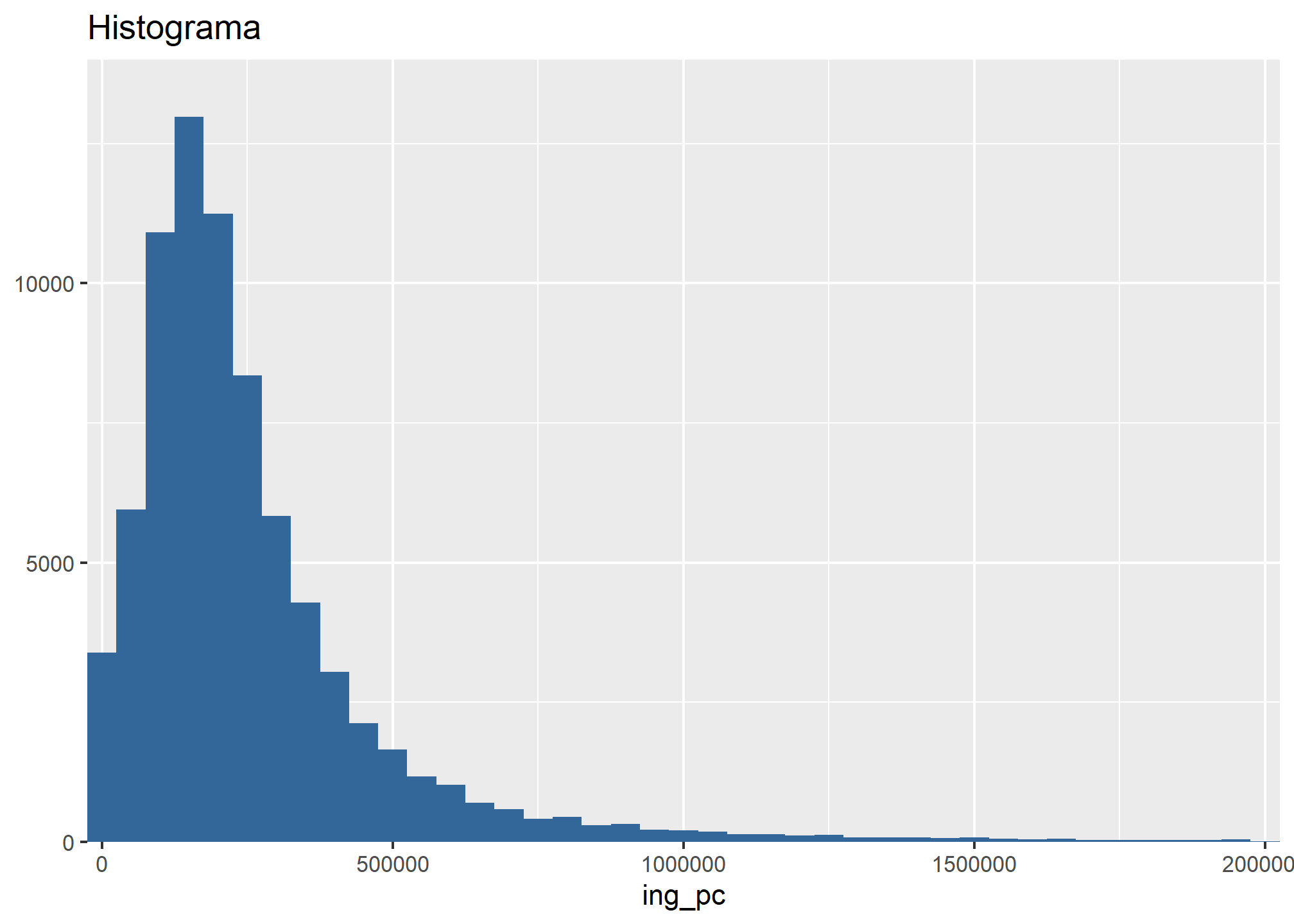
- Densidad
Ahora que vemos la distribución del histograma ¿cómo podemos graficar su densidad? es muy simple: podemos generar un gráfico de densidad con el siguiente código
datos_proc %>% filter(ing_pc <= 2000000) %>%
plot_frq(., ing_pc,
title = "Gráfico de densidad",
type = "density")
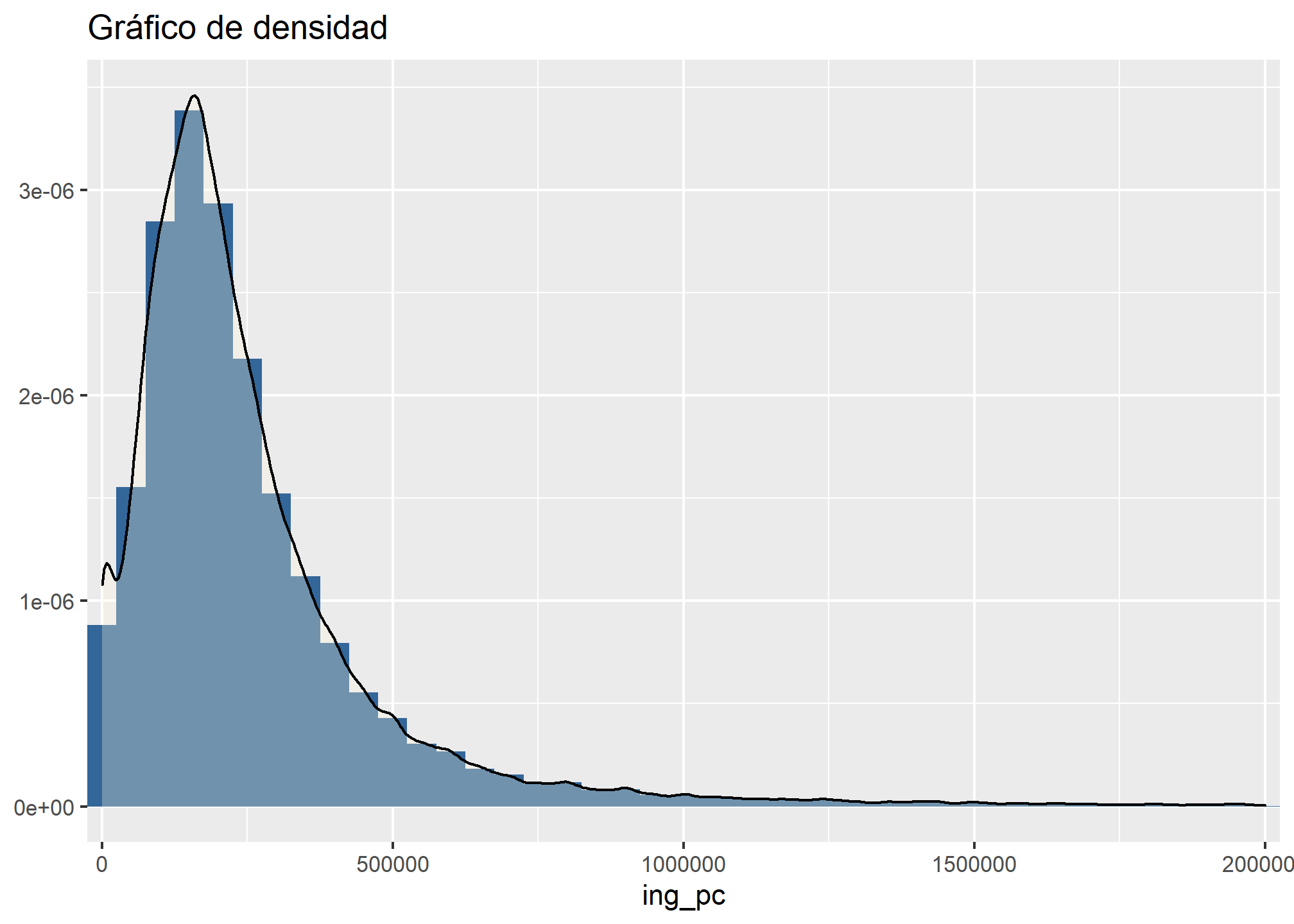
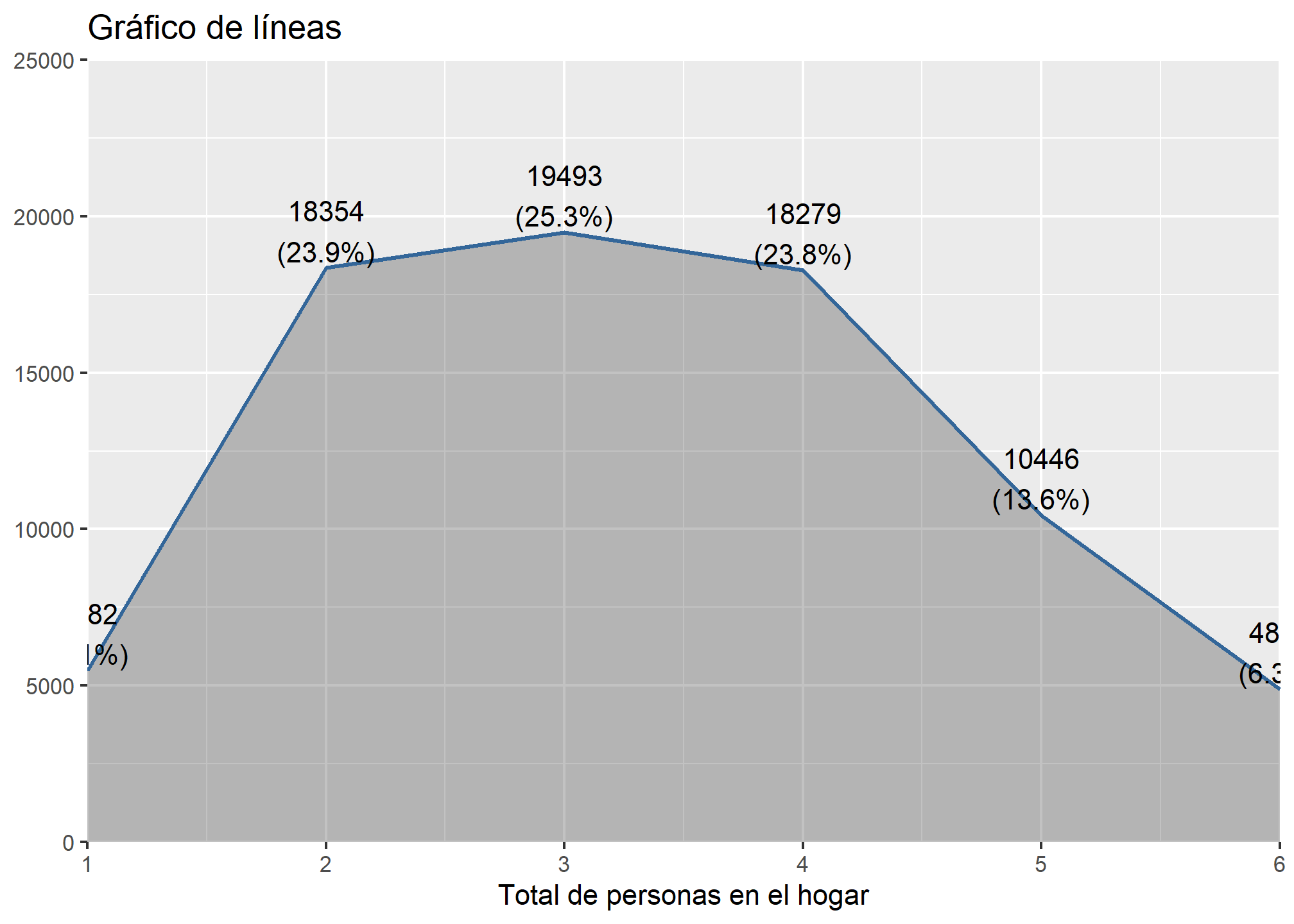
- Gráfico de líneas
¿Que pasa si me piden un gráfico de lineas?, también hay una función para eso. En esta ocasión queremos graficar la variable ife, para lo que usaremos este código:
plot_frq(datos_proc, tot_per,
title = "Gráfico de líneas",
type = "line")
- Gráfico de cajas
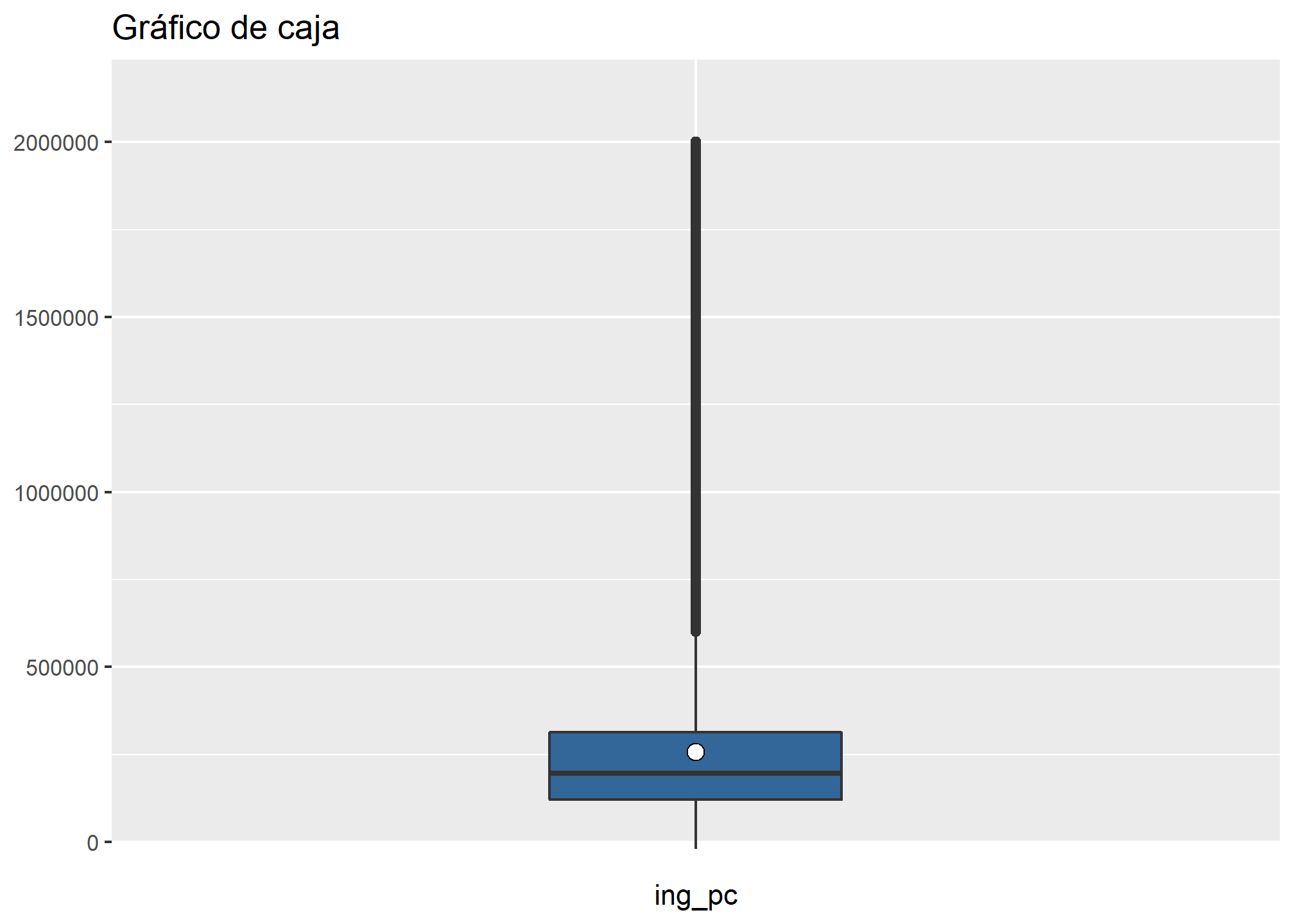
Para graficar algunas medidas de posición de una variable y, en específico, los cuartiles de esta, podemos elaborar un gráfico de cajas, para lo cual usaremos este código:
datos_proc %>% filter(ing_pc <= 2000000) %>%
plot_frq(., ing_pc,
title = "Gráfico de caja",
type = "boxplot")
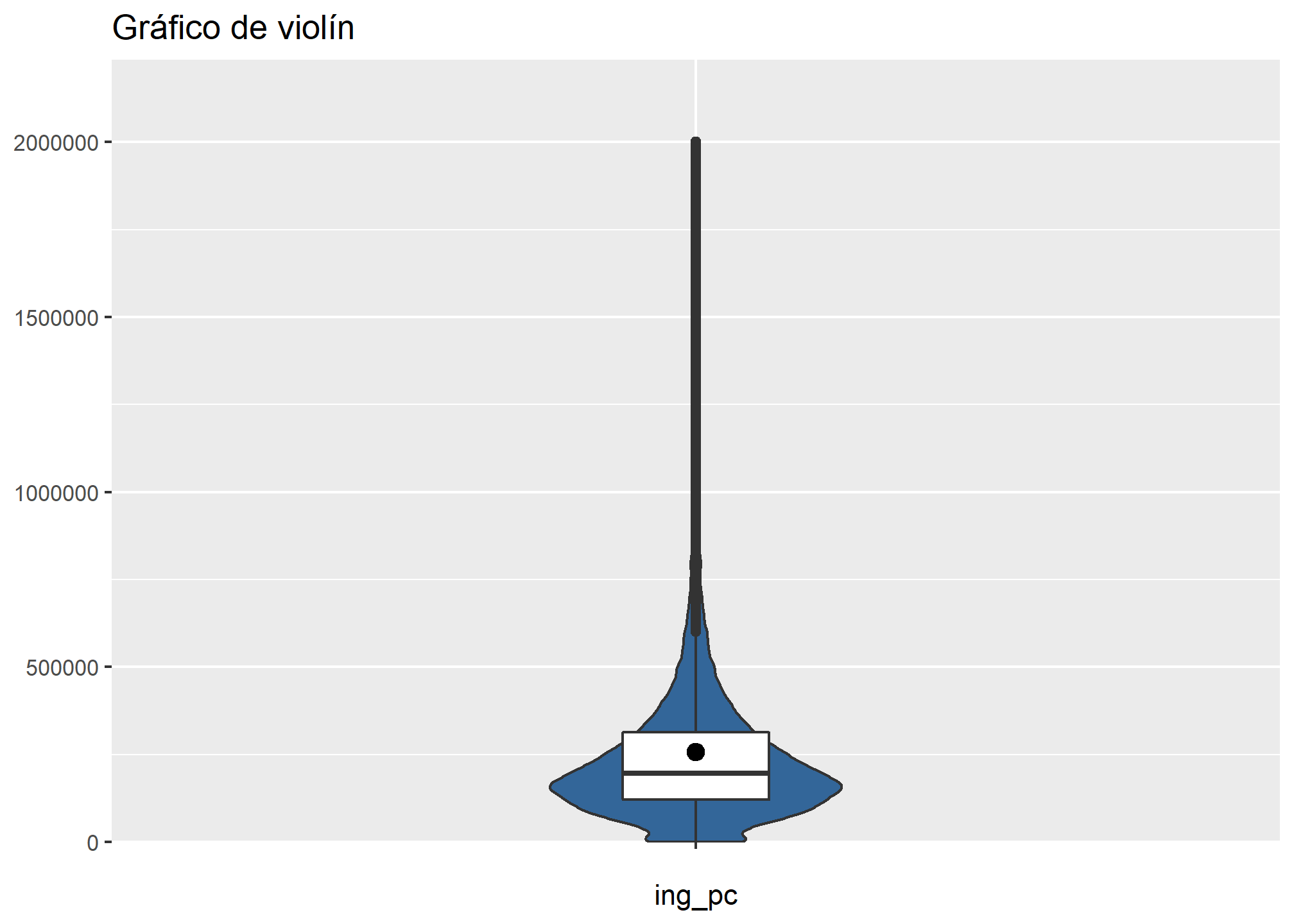
- Gráfico de violín
Finalmente, si queremos presentar gráficos de violín, usamos este código
datos_proc %>% filter(ing_pc <= 2000000) %>%
plot_frq(., ing_pc,
title = "Gráfico de violín",
type = "violin")
Como pueden ver, el único argumento que se modificaba era type = : es decir, para hacer diversos gráficos, sólo se debe especificar el tipo de gráfico que queremos, y luego personalizarlo según nuestro requerimientos, especificando el resto de argumentos.
6. Resumen del práctico
¡Eso es todo por este práctico! Hoy aprendimos a:
- Estimar estadísticos de medidas de tendencia central, posición y dispersión para variables cuantitativas
- Calcular las frecuencias absolutas y relativas para cada una de las categorías de respuesta con variables cualitativas
- Presentar ambas estimaciones
- Generar y personalizar gráficos descriptivos univariados para variables categóricas y continuas