Análisis descriptivo bivariado
0. Objetivo del práctico
El presente práctico constituye la continuación del práctico 7, por lo cual profundizaremos la presentación de tablas y gráficos descriptivos bivariados. Para esto ya debemos contar con datos previamente procesados del práctico N°6. Previo a eso, siempre es importante que recordemos en qué parte del proceso estamos

Recursos del práctico
Tal como en el práctico anterior, utilizaremos los datos procesados CASEN 2020, que proviene de los datos originales de Encuesta de Caracterización Socioeconómica (CASEN).Recuerden siempre consultar el libro códigos antes de trabajar datos.
Recuerden que los archivos asociados a este práctico se pueden descargar aquí:
1. Paquetes a utilizar
Para este práctico utilizaremos principalmente, las librerías sjmisc y sjPlot.
sjmisc: esta paquete tiene múltiples funciones, desde la transformación de datos y variables. Este paquete suele complementar a dplyr de tidyverse en sus funciones.
sjPlot: su principal función es la visualización de datos para estadística en ciencias sociales mediante tablas y gráficos.
Cargaremos los paquetes con pacman, si aún tienes dudas sobre cómo trabajar con pacman puedes revisar el práctico 2
pacman::p_load(sjmisc,
sjPlot,
tidyverse,
magrittr)2. Importar datos
Una vez cargado los paquetes a utilizar, debemos pasar al segundo paso: cargar los datos. Como indicamos al inicio, seguiremos utilizando los datos CASEN que fue procesada en el práctico anterior, pero le añadimos una variable.
load("output/data/datos_proc.RData")3. Explorar datos
¡Recordemos las variables con las que trabajaremos!
sjPlot::view_df(datos_proc,
encoding = "UTF-8")| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | folio | Identificación hogar (comuna area seg viv hogar) | range: NA-NA | |
| 2 | sexo |
Masculino Femenino |
||
| 3 | edad | Edad | range: 15-110 | |
| 4 | ocupacion | o1. La semana pasada, ¿trabajó al menos una hora? |
SÃ No |
|
| 5 | ytoth | Ingreso total del hogar | range: 0-92666667 | |
| 6 | tot_per | Total de personas en el hogar | range: 1-6 | |
| 7 | ife |
y26d_hog. Últimos 12 meses, ¿alguien recibió Ingreso Familiar de Emergencia? |
SÃ No No sabe |
|
| 8 | o2 |
o2. Aunque no trabajó la semana pasada, ¿realizó alguna actividad? |
SÃ No |
|
| 9 | o3 |
o3. Aunque no trabajó, ¿tenÃa algún empleo del cual estuvo ausente temporalmente |
SÃ No |
|
| 10 | o4 | o4. ¿Ha trabajado alguna vez? |
SÃ No |
|
| 11 | o6 |
o6. ¿Buscó trabajo remunerado o cuenta propia en las últimas cuatro semanas? |
SÃ No |
|
| 12 | ife_d | range: 0-0 | ||
| 13 | sexo_edad_tramo | <output omitted> | ||
| 14 | ing_pc | range: 0.0-18533333.4 | ||
4. Descripción de variables
Muchas veces, nuestras preguntas de investigación van más allá de la descripción de una única variable (por ejemplo ¿cómo se distribuyen los ingresos per cápita en la población analizada?). Es por ello que volveremos a hacer uso de las funciones de sjPlot ¡esta vez para descripciones que incluyen dos variables! (¡o más!).
4.1 Gráficos de dispersión
Podemos graficar la distribución en dos variables cuantitativas a la vez con la función plot_scatter, que muestra el diagrama de dispersión de tales variables, lo cual nos puede permitir explorar la existencia de relaciones entre ambas.
datos_proc %>% filter(ing_pc <= 2000000) %>%
plot_scatter(., tot_per, ing_pc)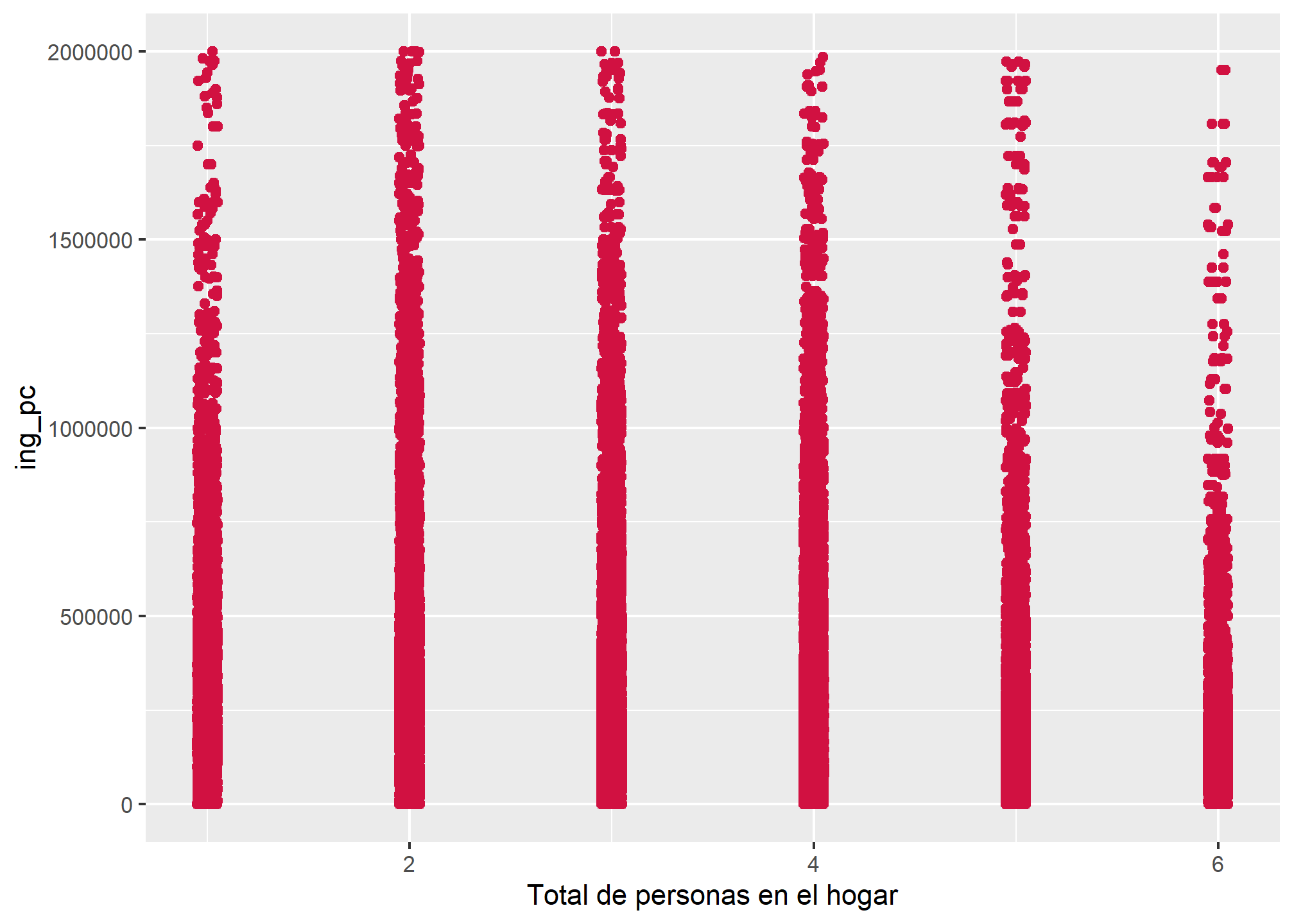
¡También es posible agregar una tercera variable categórica al diagrama de dispersión! probemos con sexo
datos_proc %>% filter(ing_pc <= 2000000) %>%
plot_scatter(., tot_per, ing_pc, sexo)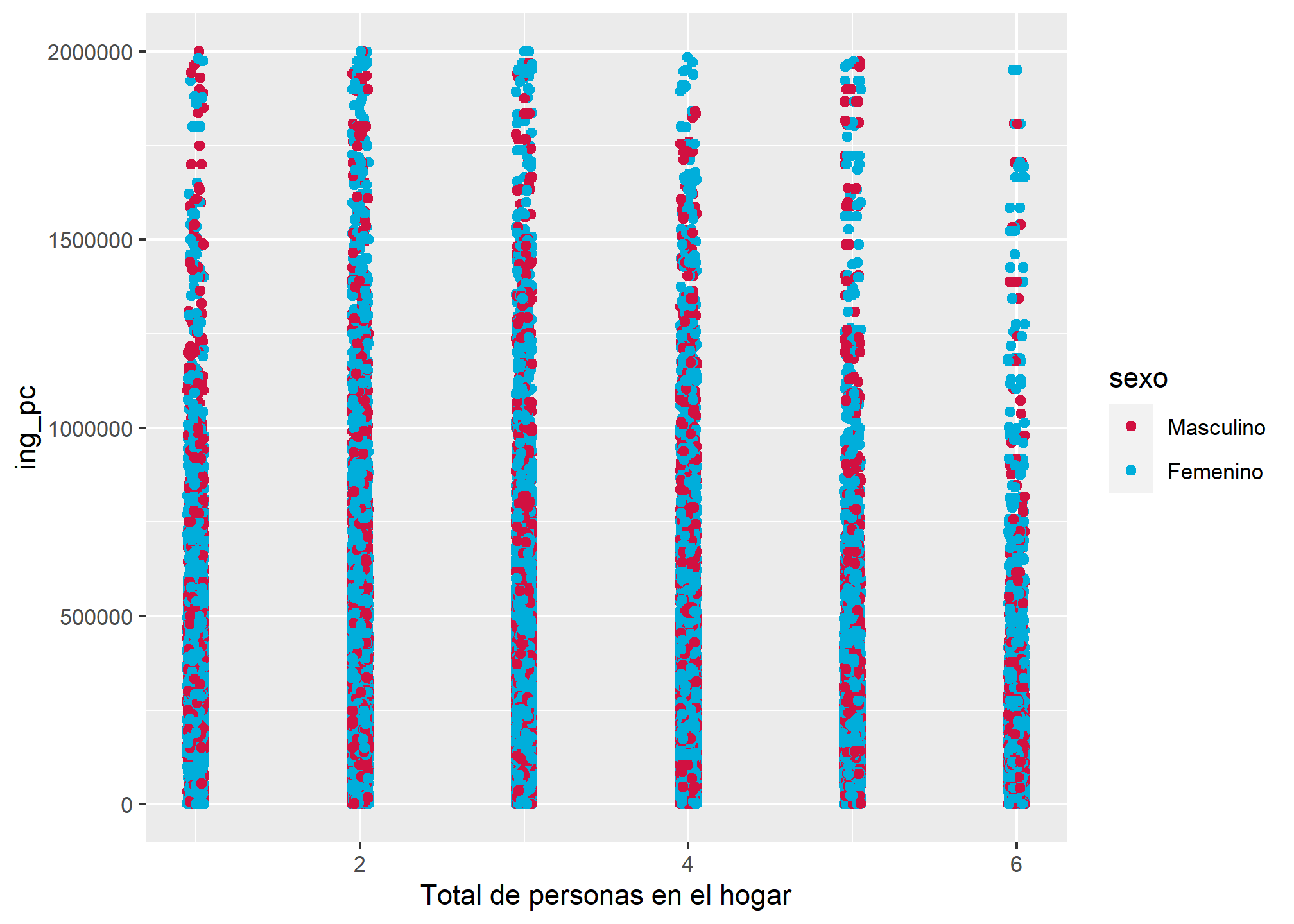
Incorporemos la línea de mínimos cuadrados ordinarios, y separemos un gráfico para cada categoría de sexo con el argumento grid =
datos_proc %>% filter(ing_pc <= 2000000) %>%
plot_scatter(., tot_per, ing_pc, sexo,
fit.grps = "lm", grid = TRUE)
4.2 Frecuencias agrupadas para variables categóricas
Ahora que ya hemos graficado las frecuencias de las variables, vamos a graficar frecuencias agrupadas, para ello usaremos la función plot_grpfrq de sjPlot, que se estructura de la presente forma
plot_grpfrq(
var.cnt,
var.grp,
type = c("bar", "dot", "line", "boxplot", "violin")- Gráfico de barras
La primera opción que nos entrega este código son los gráficos de barra. Si queremos saber cuántos hombres y mujeres trabajaron al menos una hora la semana pasada, graficaremos las variables sexo y o4
plot_grpfrq(datos_proc$sexo, datos_proc$o4,
type = "bar", title = "Gráfico de barras")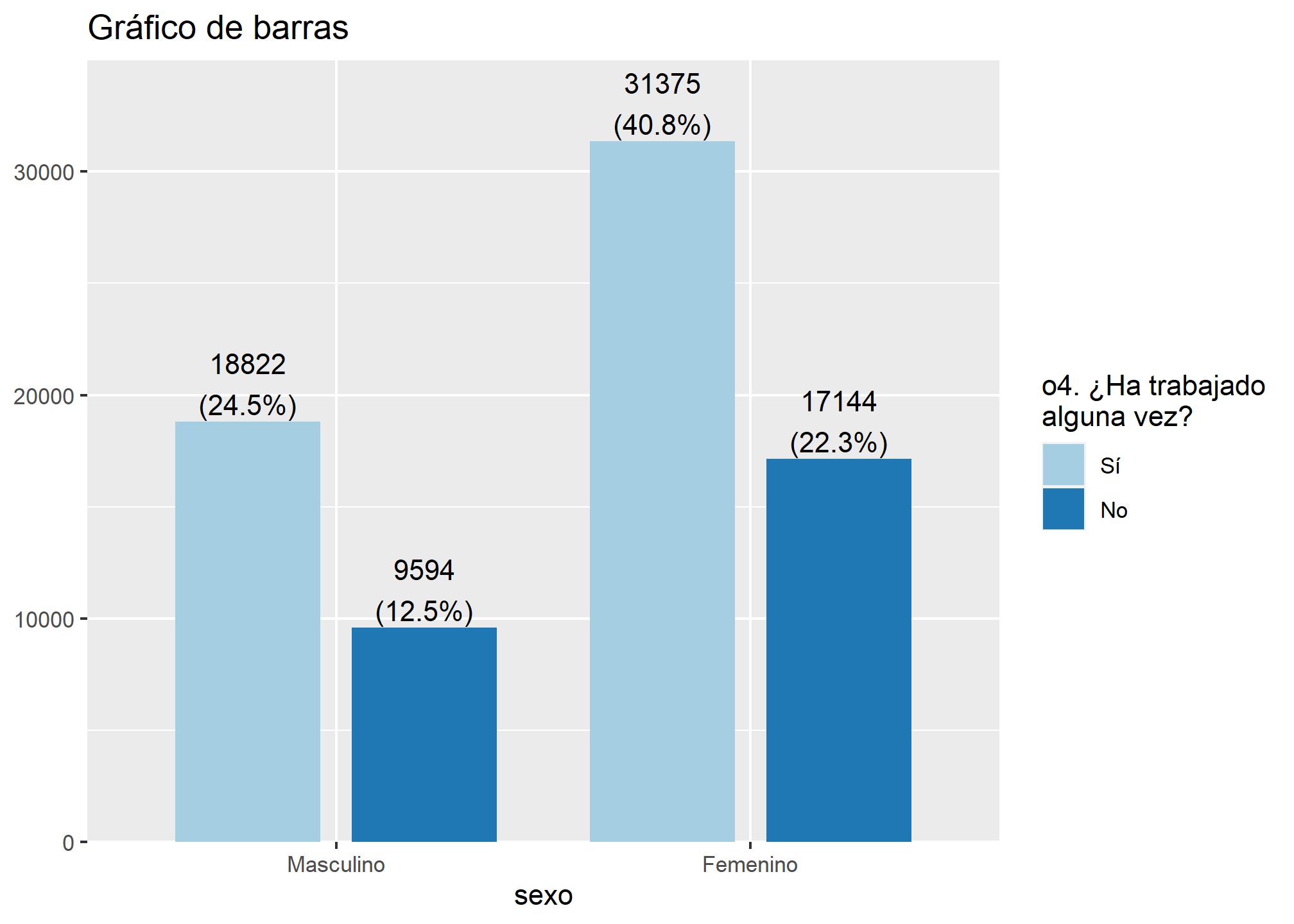
Podemos ver que no solo nos muestra la frecuencia absoluta, sino que también la frecuencia relativa en porcentaje
Además, podemos incorporar una tercera barra que presenta el total de ambas categorías. Así, sabremos cuántas/os adultas/os, adultas/os mayores y jóvenes (mujeres y hombres) han trabajado al menos una vez o no, y qué proporción del total de informantes representa cada una de las categorías de edad y sexo
Para este ejercicio usaremos la función plot_xtab(), de la misma librería
plot_xtab(datos_proc$sexo_edad_tramo, datos_proc$o4, title = "Gráfico de barras")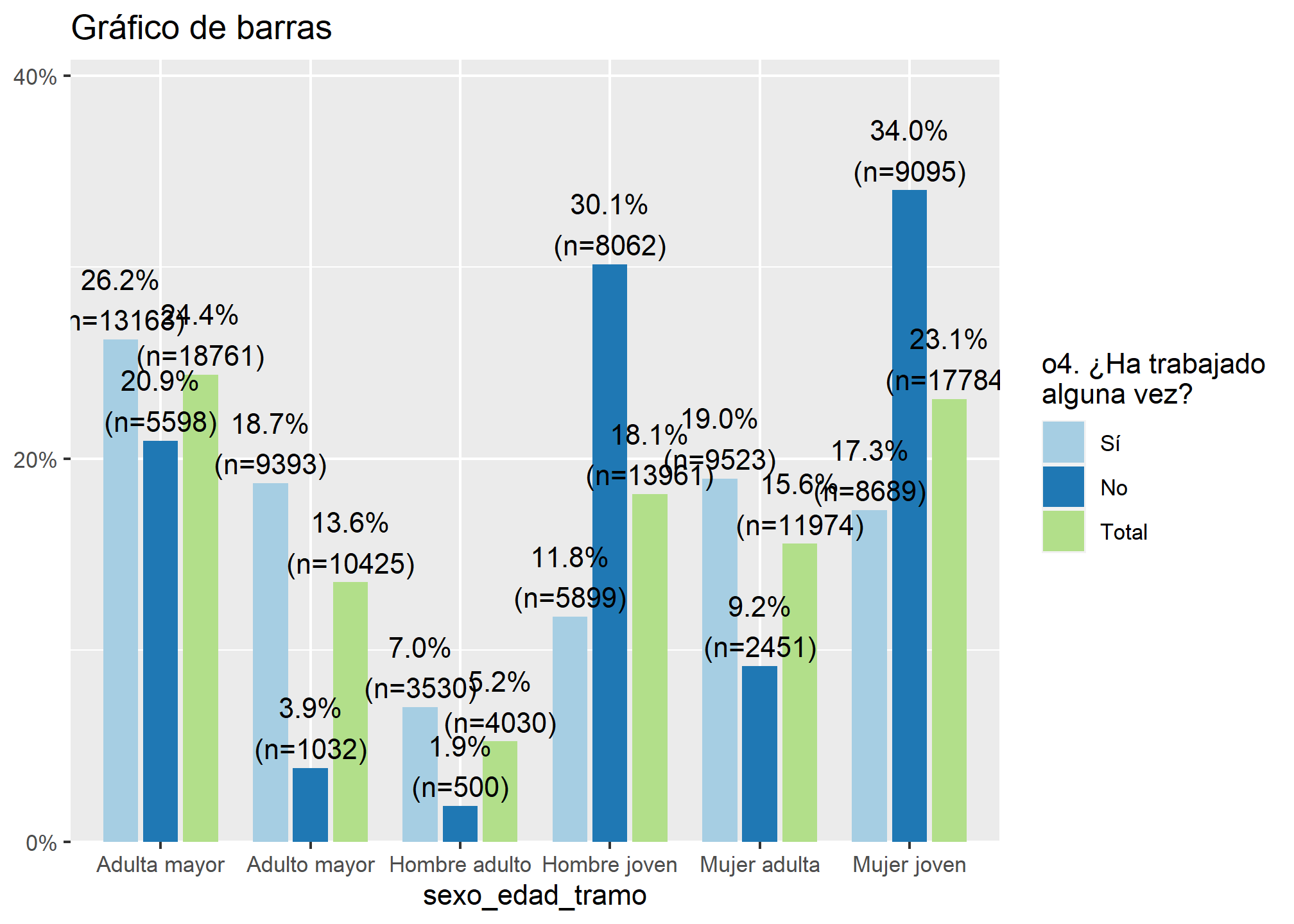
1.1 Gráfico de barras horizontales
Con la misma función podemos graficar mediante barras horizontales con el argumento coord.flip =. Además show.summary = nos muestra estadísticos de la relación entre las variables
plot_xtab(datos_proc$o4, datos_proc$sexo_edad_tramo, margin = "row",
bar.pos = "stack",
title = "Gráfico de barras horizontales",
show.summary = TRUE, coord.flip = TRUE)
También es posible graficar diversas variables que presentan las mismas categorías de respuesta (en este caso, Sí, No y NA) para ver diferencias en las distribuciones para cada una. Utilicemos la función plot_stackfrq de sjPlot
datos_proc %>% select(ocupacion, o2, o3, o4, o6) %>%
plot_stackfrq(., title = "Gráfico de barras proporcional")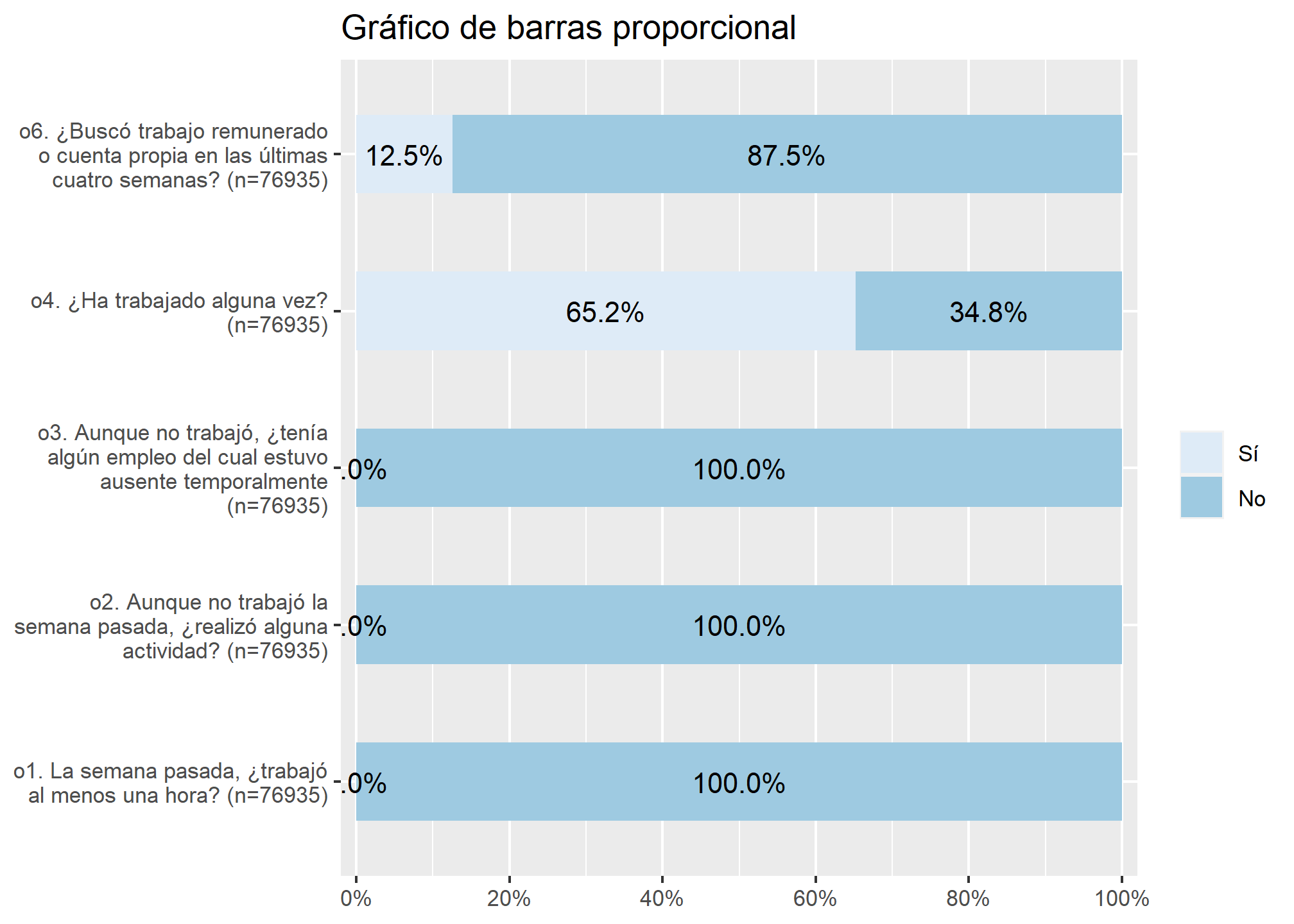
1.2 Escalas Likert
También podemos graficar escalas Likert, lo cual es una gran herramienta para quienes trabajamos en ciencias sociales. En esta ocasión CASEN no tiene variables con más categorias de respuesta para generar una escala Likert, por lo que utilizaremos las nuevas variables de la base procesada. Generemos el gráfico con la función plot_likert()
datos_proc %>% select("ocupacion","o2", "o3", "o4", "o6") %>%
sjPlot::plot_likert(., title = "Gráfico de escalas Likert")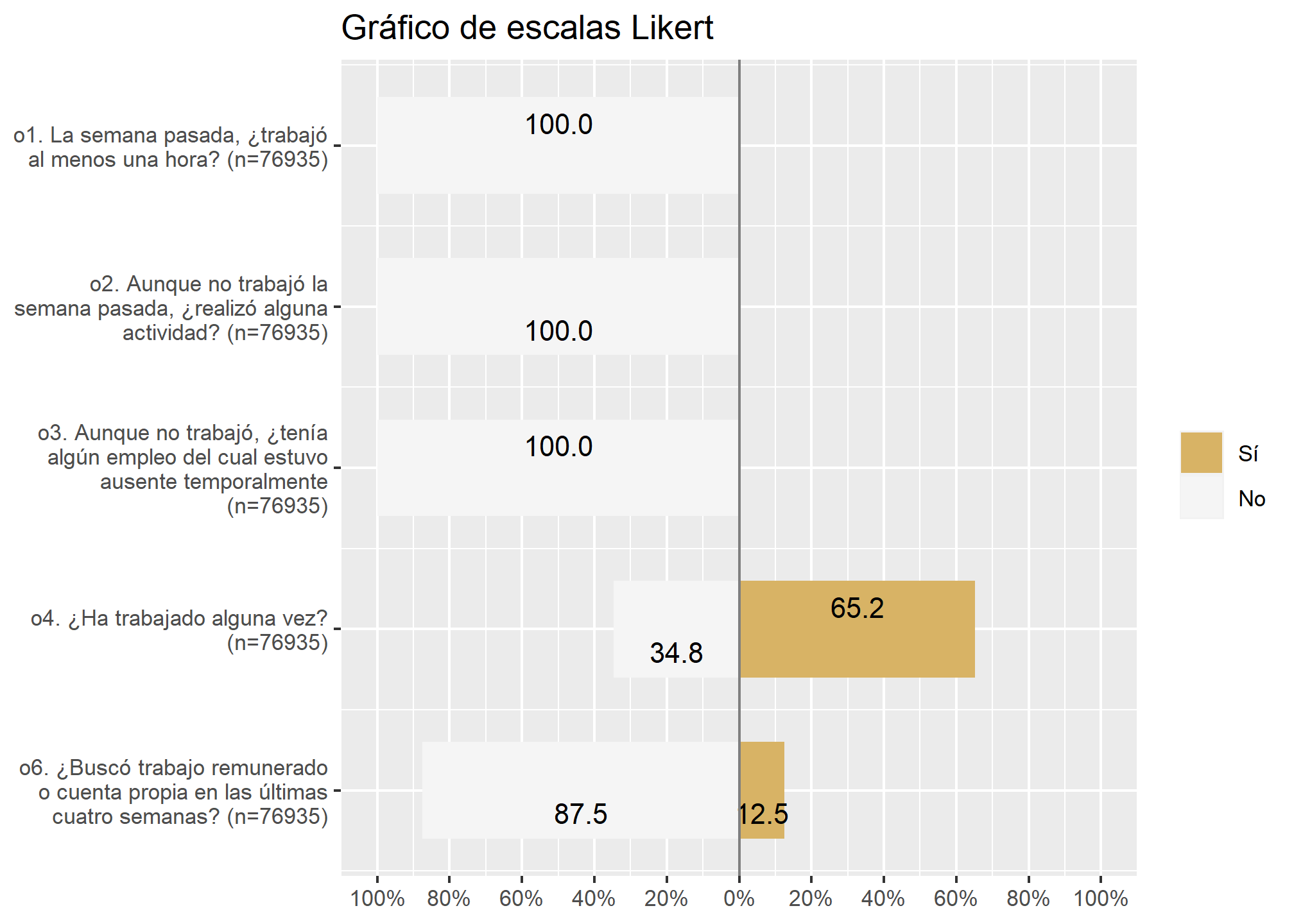
1.3 Tablas de proporción cruzadas
Con plot_gpt(), se puede graficar tablas cruzadas proporcionales agrupadas. Este código traza la proporción de cada nivel de x (o4) para la categoría más alta en y (o6), para cada subgrupo de grp (sexo).
plot_gpt(datos_proc, o4, o6, sexo,
shapes = c(15, 21),
title = "Gráfico de proporción agrupada")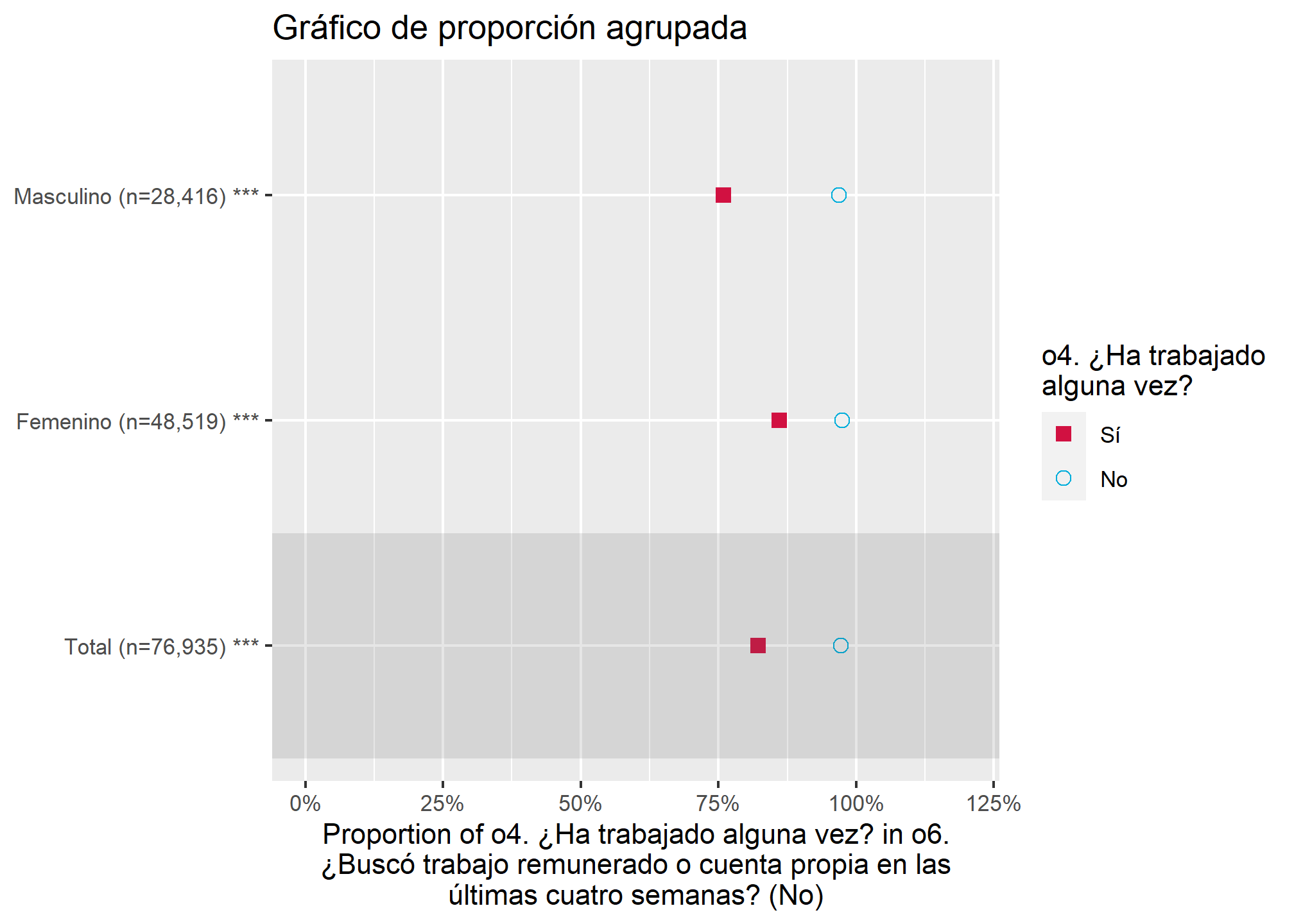
- Gráfico de puntos
Ahora continuaremos con los gráficos de puntos, ya que quiero presentar la relación entre sexo y o4 mediante otro gráfico:
plot_grpfrq(datos_proc$sexo, datos_proc$o4,
title = "Gráfico de puntos",
type = "dot")
- Gráfico de líneas
Otra opción que tiene esta función es la creación de gráficos de líneas. Para ello conoceremos la relación entre el tramo sexo-edad y el haber trabajado alguna vez
plot_grpfrq(datos_proc$sexo_edad_tramo, datos_proc$o4,
title = "Gráfico de línea",
type = "line")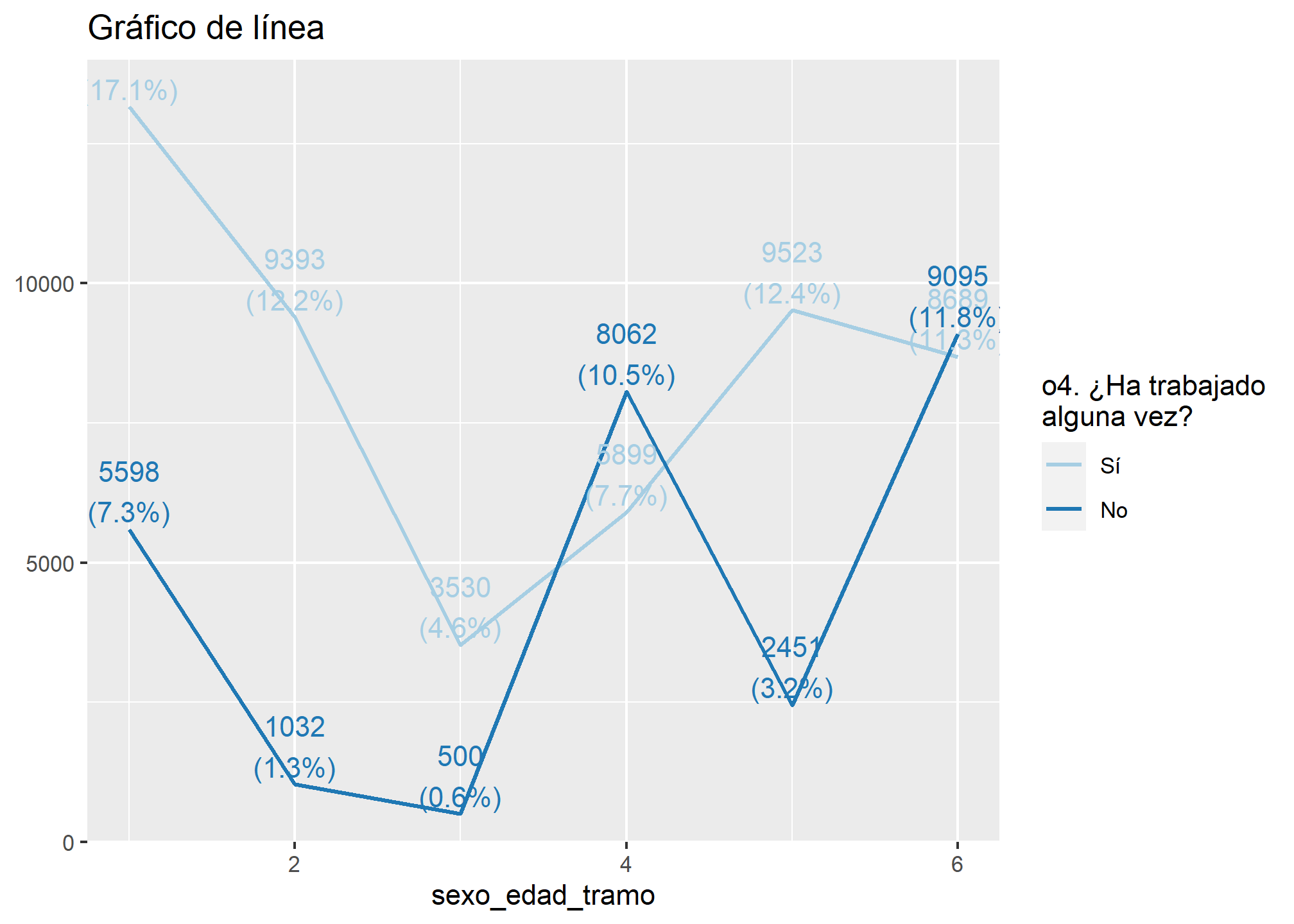
- Gráfico de cajas
Ahora, si queremos conocer cómo interactúan el total de personas habitantes del hogar con el tramo sexo-etario, podemos visualizarlo mediante un gráfico de cajas
plot_grpfrq(datos_proc$tot_per, datos_proc$sexo_edad_tramo,
title = "Gráfico de caja",
type = "boxplot")
Además, se puede incorporar una tercera variable, en este caso lo haremos con la variable o4 y el argumento intr.var =
plot_grpfrq(datos_proc$tot_per, datos_proc$sexo_edad_tramo, intr.var = datos_proc$o4,
title = "Gráfico de cajas",
type = "box")
- Gráfico de violín
Finalmente, para generar un gráfico de violín, añadiremos el argumento type = "violin"
plot_grpfrq(datos_proc$tot_per, datos_proc$sexo_edad_tramo,
title = "Gráfico de violín",
type = "violin")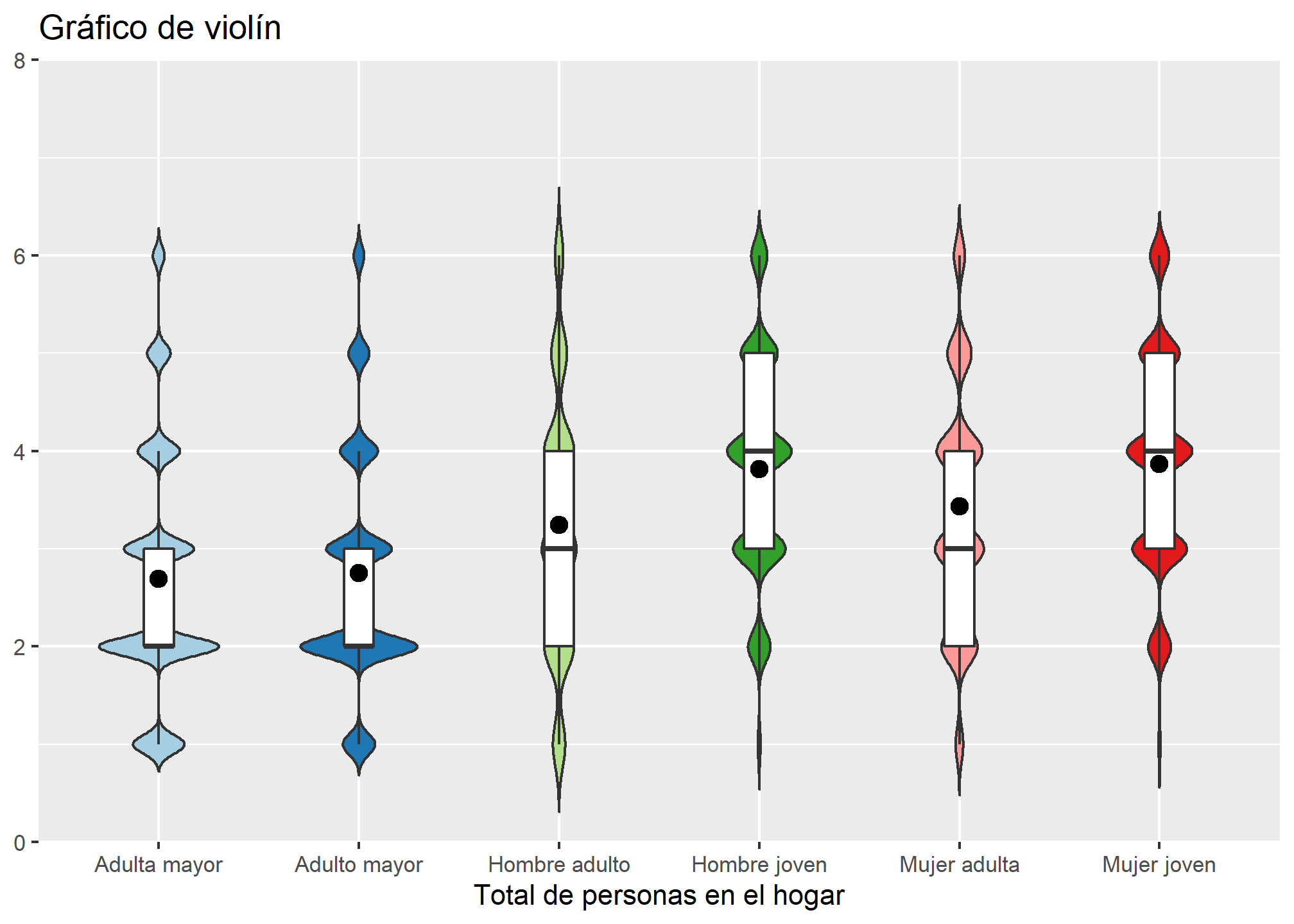
Nuevamente, la función nos permite la creación de múltiples gráficos ¡sólo se debe cambiar el argumento type =!
4.3 Tablas de contingencia
¡No podemos terminar sin saber cómo hacer tablas de frecuencias cruzadas!
Por suerte sjPlot tiene la función sjt.xtab, que nos entrega tablas de frecuencias cruzadas
sjt.xtab(datos_proc$sexo, datos_proc$o4,
show.col.prc=TRUE,
show.summary=FALSE,
title = "Tabla de contingencia")| sexo |
o4. ¿Ha trabajado alguna vez? |
Total | |
|---|---|---|---|
| SÃ | No | ||
| Masculino |
18822 37.5 % |
9594 35.9 % |
28416 36.9 % |
| Femenino |
31375 62.5 % |
17144 64.1 % |
48519 63.1 % |
| Total |
50197 100 % |
26738 100 % |
76935 100 % |
¿Qué pasó? ¿por qué salen esos símbolos raros en la tabla?
¡Es por la codificación!, para ello le agregamos el argumento encoding = "UTF-8" y ya tenemos nuestra tabla de frecuencias cruzadas
sjt.xtab(datos_proc$sexo, datos_proc$o4,
show.col.prc=TRUE,
show.summary=FALSE,
encoding = "UTF-8",
title = "Tabla de contingencia")| sexo |
o4. ¿Ha trabajado alguna vez? |
Total | |
|---|---|---|---|
| SÃ | No | ||
| Masculino |
18822 37.5 % |
9594 35.9 % |
28416 36.9 % |
| Femenino |
31375 62.5 % |
17144 64.1 % |
48519 63.1 % |
| Total |
50197 100 % |
26738 100 % |
76935 100 % |
Si además se quieren añadir variables con las mismas categorías de respuesta, se puede utilizar la función tab_stackfrq(). Para ello utilizaremos las variables añadidas para este práctico: o3, o4 y o6. Le añadiremos etiquetas con value.labels y le pediremos que nos entregue la frecuencia absoluta (show.n = TRUE) y el total (show.total = T)
tab_stackfrq(as.data.frame(datos_proc %>% select("o3", "o4", "o6")),
value.labels=c('1'='Si', '2'='No'),
show.n = TRUE, show.total = T,
file = "output/figures/tabla4.doc")| Si | No | N | |
|---|---|---|---|
|
o3. Aunque no trabajó, ¿tenÃa algún empleo del cual estuvo ausente temporalmente |
0 (0.00 %) |
76935 (100.00 %) |
76935 |
|
o4. ¿Ha trabajado alguna vez? |
50197 (65.25 %) |
26738 (34.75 %) |
76935 |
|
o6. ¿Buscó trabajo remunerado o cuenta propia en las últimas cuatro semanas? |
9644 (12.54 %) |
67291 (87.46 %) |
76935 |
5. Test de independencia Chi2
A la hora de graficar Chi2, debemos asegurarnos con la función as_factor que las variables a utilizar sean de tipo factor, luego utilizamos la función sjp.chi2 de sjPlot para crear la tabla, finalmente con el argumento axis.labels asignamos la etiqueta de cada variable
data.frame(as_factor(sample(datos_proc$sexo, replace = TRUE)),
as_factor(sample(datos_proc$o4, replace = TRUE)),
as_factor(sample(datos_proc$o6, replace = TRUE))) %>%
sjp.chi2(.,
title = "Gráfico de Chi2",
axis.labels = c("Ha trabajado alguna vez", "Busco empleo"))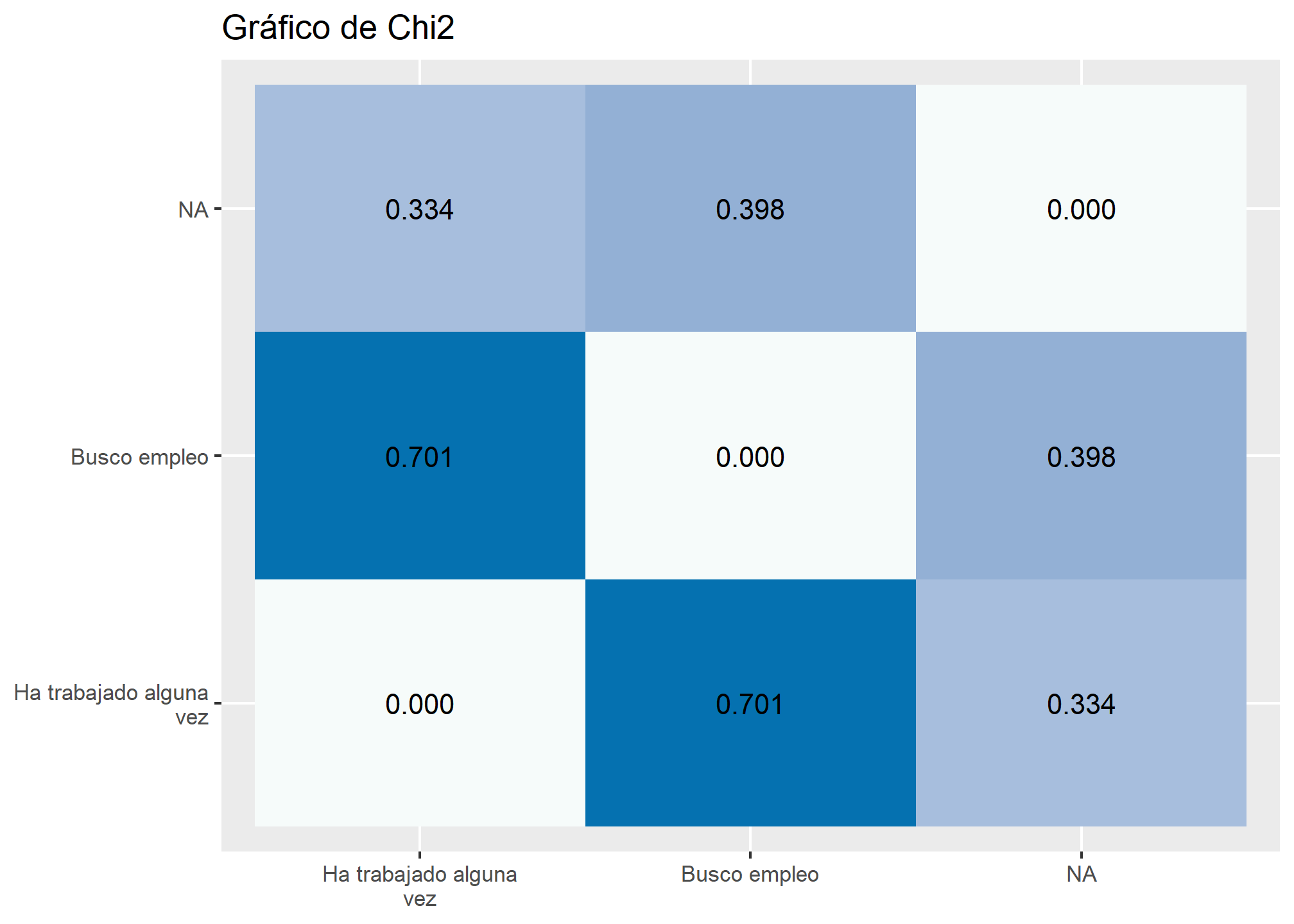
6. Correlación
Ahora veremos estadísticos bivariados, como la correlación, en esta ocasión generaremos una tabla de correlación entre las variables tot_per y ing_pc, para eso usaremos la función tab_corr de sjPlot
Previamente debemos seleccionar las variables a utilizar, ya que no tiene sentido incluir en el análisis variables nominales
datos_proc %>%
select(ing_pc, tot_per) %>%
tab_corr(.,
triangle = "lower",
title = "Tabla de correlación",
encoding = "UTF-8")| ing_pc | Total de personas en el hogar | |
|---|---|---|
| ing_pc | ||
| Total de personas en el hogar | -0.125*** | |
| Computed correlation used pearson-method with listwise-deletion. | ||
7. Anova
Finalmente, si queremos reportar un análisis de Anova, no podemos dejar de lado este gráfico que nos otorga la función sjp.aov1 del paquete sjPlot
sjp.aov1(datos_proc$ing_pc, datos_proc$sexo, title = "Anova")
8. Resumen del práctico
¡Eso es todo por este práctico! Hoy aprendimos a:
- Manejar datos descriptivos en RStudio
- A obtener tablas descriptivas bivariadas
- A visualizar los descriptivos bivariados
- A obtener tablas de contingencia
- A obtener tablas de correlación y chi2
- A obtener gráficos de Anova