Regresiones lineales
0. Objetivo de la práctica
El objetivo del práctico, es avanzar en la etapa de análisis de los datos a través del uso de regresiones lineales. Para esto usaremos datos previamente procesados de la base de datos a utilizar. ¡No olvidemos que nos encontramos en el análisis de datos!

Entonces, en esta práctica aprenderemos trabajar las regresiones lineales, trabajando con predictores continuos y categóricos. Luego veremos las diferencias de la estimación simple con pesos muestrales, para continuar con la extracción de objetos y finalmente veremos como representarlos mediante gráficos y tablas.
1. Recursos del práctico
En este práctico utilizamos los datos procesados de la Encuesta Suplementaria de Ingresos (ESI) 2020.Recuerden siempre consultar el libro códigos antes de trabajar datos.
2. Paquetes a utilizar
En este práctico utilizaremos siete paquetes
-
pacman: este facilita y agiliza la lectura de los paquetes a utilizar en R; -
tidyverse: colección de paquetes; -
srvyr: para crear el objeto encuesta; -
survey: para crear modelos incorporando el diseño muestral; -
sjPlot: para presentar tablas y gráficos con los modelos creados;
pacman::p_load(sjPlot,
tidyverse,
srvyr,
survey)
3. Importar datos
Una vez cargado los paquetes a utilizar, debemos cargar los datos procesados.
datos <- readRDS("output/data/datos_proc.rds")
4. Explorar datos
Es relevante explorar los datos que utilizaremos, cómo están previamente procesados ¡no sabemos con que variables estamos trabajando!
names(datos)
## [1] "ing_t_t" "edad" "sexo" "est_conyugal" "ciuo08"
## [6] "fact_cal_esi"
head(datos)
## # A tibble: 6 x 6
## ing_t_t edad sexo est_conyugal ciuo08 fact_cal_esi
## <dbl> <dbl> <dbl+lbl> <chr> <dbl+lbl> <dbl>
## 1 320421. 29 2 [Mujer] Con pareja 5 [Trabajadores de los se~ 346.
## 2 750000 30 2 [Mujer] Sin pareja 2 [Profesionales, científ~ 1056.
## 3 900000 43 2 [Mujer] Sin pareja 2 [Profesionales, científ~ 41.6
## 4 0 15 2 [Mujer] Sin pareja NA 265.
## 5 0 11 1 [Hombre] <NA> NA 282.
## 6 0 62 2 [Mujer] Sin pareja NA 165.
Ahora sabemos que trabajaremos con seis variables: "ing_t_t", "est_conyugal", "ciuo08", "sexo", "edad" y "fact_cal_esi",. Ahora inclusive podemos explorar nuestros datos con sjPlot::view_df()
sjPlot::view_df(datos,
encoding = "UTF-8")
| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | ing_t_t | Total ingresos del trabajo | range: 0.0-18045761.6 | |
| 2 | edad | Edad de la persona | range: 0-106 | |
| 3 | sexo | Sexo | 1 2 |
Hombre Mujer |
| 4 | est_conyugal | <output omitted> | ||
| 5 | ciuo08 | b1. Grupo ocupacional según CIUO 08 - 1 dÃgito | 1 2 3 4 5 6 7 8 9 10 999 |
Directores, gerentes y administradores Profesionales, cientÃficos e intelectuales Técnicos y profesionales de nivel medio Personal de apoyo administrativo Trabajadores de los servicios y vendedores de comercios y mercados Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros Artesanos y operarios de oficios Operadores de instalaciones, maquinas y ensambladores Ocupaciones elementales Otros no identificados Sin clasificación |
| 6 | fact_cal_esi | Factor de expansión ESI con nueva calibración, proyecciones de población |
range: 2.8-7070.1 | |
Perfecto, podemos ver las variables que tenemos y sus categorías de respuesta pasaremos a la regresión
5. Modelo de regresión lineal
5.1 Formula
Previo a eso recordemos que la fórmula de la regresión lineal simple es:
\begin{equation} \widehat{Y}=b_{0} +b_{1}X \end{equation}
Mientras que en la regresión lineal múltiple es:
\begin{equation} \widehat{Y}=b_{0} +b_{1}X +b_{2}X +b_{x}X \end{equation}
Donde
\(\widehat{Y}\)es el valor estimado/predicho de\(Y\)\(b_{0}\)es el intercepto de la recta (el valor de Y cuando X es 0)\(b_{1}\)y\(b_{2}\)son los coeficiente de regresión, que nos dice cuánto aumenta Y por cada punto que aumenta X (pendiente)
Ecuaciones en LateX
Previo a revisar regresiones en R, es necesario aprender cómo están hechas estas ecuaciones
Hay dos maneras de realizarlo. Para ello será muy importante el signo $. Para entenderlo usaremos el ejemplo que está arriba
Forma 1 de ecuación: Esta forma se utiliza para que la fórmula esté centrada en una linea específica
\begin{equation}
\widehat{Y}=b_{0} +b_{1}X
\end{equation}
- Resultado
\begin{equation} \widehat{Y}=b_{0} +b_{1}X \end{equation}
- Con
\begin indicamos el inicio y con las llaves ({}) especificamos que queremos escribir una ecuación {equation} \widehat especificamos la ecuación \end decimos a R que es el fin de la ecuación {equation}
Forma 2: Esta forma se utiliza para que la fórmula este de forma contínua en el texto (inline)
${Y} = b_{0} +b_{1}X$
- Resultado
\({Y}=b_{0} +b_{1}X\)
Forma 3: Con esta forma la ecuación se verá centrada
$${Y}=b_{0} +b_{1}X$$
- Resultado
$${Y}=b_{0} +b_{1}X$$
Si quieres aprender más sobre el uso de ecuaciones en LateX, dirígete acá
Les mostramos esto porque de la misma forma se diferencian ambos procedimientos en R
Para la regresión lineal simple se utiliza la siguiente estructura:
objeto <- lm(dependiente ~ independiente, data=datos)
Mientras que para la regresión lineal múltiple, sólo se añaden más variables con el signo +
objeto <- lm(dependiente ~ independiente1 + independiente 2 + independientex, data=datos)
5.2 Modelo
En este práctico no sólo aprenderemos a utilizar regresiones en R, sino que también a utilizalas con pesos muestrales. Pero, ¿cuál es la diferencia? ¡Ahora lo veremos!
Modelo nulo sin pesos muestrales
Para ello crearemos en un objeto nuestro modelo nulo
modelo0_sin <- lm(ing_t_t ~ 1,
data = datos)
y lo visualizaremos con
summary(modelo0_sin)
##
## Call:
## lm(formula = ing_t_t ~ 1, data = datos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -206355 -206355 -206355 94039 17839407
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 206355 1795 115 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 481300 on 71934 degrees of freedom
Modelo nulo con pesos muestrales
Luego crearemos el modelo con peso muestral, para esto debemos añadir un nuevo argumento weights, donde se especifica el factor de expansión
modelo0 <- lm(ing_t_t ~ 1,
data = datos,
weights = fact_cal_esi)
Ahora veremos los resultados con
summary(modelo0)
##
## Call:
## lm(formula = ing_t_t ~ 1, data = datos, weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -21542431 -3770518 -2542853 488353 328574529
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 256201 2090 122.6 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9240000 on 71934 degrees of freedom
Entonces ¿qué diferencias hay?
summary(modelo0);summary(modelo0_sin)
##
## Call:
## lm(formula = ing_t_t ~ 1, data = datos, weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -21542431 -3770518 -2542853 488353 328574529
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 256201 2090 122.6 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9240000 on 71934 degrees of freedom
##
## Call:
## lm(formula = ing_t_t ~ 1, data = datos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -206355 -206355 -206355 94039 17839407
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 206355 1795 115 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 481300 on 71934 degrees of freedom
Utilizando ecuaciones en LateX, se vería de la siguiente manera
Modelo sin muestral
\begin{equation} \widehat{Y}= 206355 + b_{1}X \end{equation}
Modelo con peso muestral
\begin{equation} \widehat{Y}= 256201 + b_{1}X \end{equation}
Hay diferencias en el intercepto y en los errores estándar, ya que uno asume pesos de precisión y otro asume pesos muestrales.
Por ello es muy importante incorporar el peso muestral en el análisis, sino los estimadores puntuales no serán exactos, no podremos realizar inferencia a nivel poblacional a partir del modelo, debido a la sobrestimación de la precisión de los estimadores.
5.3 Regresión lineal simple
Ahora estimaremos modelos simples
El primero sera entre ingresos y edad (ing_t_t, edad)
modelo1 <- lm(ing_t_t ~ edad,
data = datos,
weights = fact_cal_esi)
summary(modelo1)
##
## Call:
## lm(formula = ing_t_t ~ edad, data = datos, weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -21658308 -3745508 -2285119 35317 329034133
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 127658.05 4042.33 31.58 <2e-16 ***
## edad 3511.38 94.84 37.03 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9153000 on 71933 degrees of freedom
## Multiple R-squared: 0.0187, Adjusted R-squared: 0.01869
## F-statistic: 1371 on 1 and 71933 DF, p-value: < 2.2e-16
Ecuación:
\begin{equation}
\widehat{Y}= b_{0} +b_{1}X
\end{equation}
Reemplazamos
\begin{equation}
\widehat{ing_t_t}= 127658.05 + 3511.38*edad
\end{equation}
Resultado:
\begin{equation} \widehat{ing_t_t}= 127658.05 + 3511.38*edad \end{equation}
También podemos ver la relación entre ingresos y sexo (ing_t_t, sexo)
modelo2_sin <- lm(ing_t_t ~ sexo,
data = datos,
weights = fact_cal_esi)
summary(modelo2_sin)
##
## Call:
## lm(formula = ing_t_t ~ sexo, data = datos, weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -27280367 -3615240 -2145275 120699 325618868
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 498448 6568 75.89 <2e-16 ***
## sexo -160784 4138 -38.86 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9145000 on 71933 degrees of freedom
## Multiple R-squared: 0.02056, Adjusted R-squared: 0.02055
## F-statistic: 1510 on 1 and 71933 DF, p-value: < 2.2e-16
¡Pero espera! ¡sexo no es una variable continua!
Predictores categóricos
Previo a esto hay que recordar que sexo no es un predictor continuo, y también debemos recordárselo a R. Este es un proceso que debe realizarse en el código de preparación, pero para ver como procesa R los predictores categóricos en una regresión lo haremos acá
Para ello utilizamos forcats un paquete del universo tidyverse con la función as_factor
datos$sexo <- forcats::as_factor(datos$sexo) #Recuerden que esto debería ir en el código de preparación
¡Vamos al modelo!
modelo2 <- lm(ing_t_t ~ sexo,
data = datos,
weights = fact_cal_esi)
summary(modelo2)
##
## Call:
## lm(formula = ing_t_t ~ sexo, data = datos, weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -27280367 -3615240 -2145275 120699 325618868
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 337664 2945 114.65 <2e-16 ***
## sexoMujer -160784 4138 -38.86 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9145000 on 71933 degrees of freedom
## Multiple R-squared: 0.02056, Adjusted R-squared: 0.02055
## F-statistic: 1510 on 1 and 71933 DF, p-value: < 2.2e-16
Como pueden ver, ahora especifica qué categoría de respuesta utiliza como nivel de referencia, esto en la variable sexo quizá puede ser intuitivo, pero ¿qué pasaría con las que tienen otras categorías de respuesta?
intentémoslo con ciuo08 y est_conyugal
datos$ciuo08 <- forcats::as_factor(datos$ciuo08)
datos$est_conyugal <- forcats::as_factor(datos$est_conyugal)
# ¡No olviden que esto debe ir en el código de procesamiento!
Modelo para ciuo08
modelo3 <- lm(ing_t_t ~ ciuo08,
data = datos,
weights = fact_cal_esi)
summary(modelo3)
##
## Call:
## lm(formula = ing_t_t ~ ciuo08, data = datos, weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -81184669 -3408145 -828630 1334160 263027210
##
## Coefficients:
## Estimate
## (Intercept) 2062790
## ciuo08Profesionales, científicos e intelectuales -925708
## ciuo08Técnicos y profesionales de nivel medio -1327327
## ciuo08Personal de apoyo administrativo -1551221
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -1687053
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -1717604
## ciuo08Artesanos y operarios de oficios -1672564
## ciuo08Operadores de instalaciones, maquinas y ensambladores -1550495
## ciuo08Ocupaciones elementales -1782209
## ciuo08Otros no identificados -1019599
## ciuo08Sin clasificación -1737325
## Std. Error
## (Intercept) 19190
## ciuo08Profesionales, científicos e intelectuales 21334
## ciuo08Técnicos y profesionales de nivel medio 21921
## ciuo08Personal de apoyo administrativo 24706
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 20888
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 30756
## ciuo08Artesanos y operarios de oficios 21957
## ciuo08Operadores de instalaciones, maquinas y ensambladores 23380
## ciuo08Ocupaciones elementales 21067
## ciuo08Otros no identificados 58328
## ciuo08Sin clasificación 118089
## t value
## (Intercept) 107.49
## ciuo08Profesionales, científicos e intelectuales -43.39
## ciuo08Técnicos y profesionales de nivel medio -60.55
## ciuo08Personal de apoyo administrativo -62.79
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -80.77
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -55.85
## ciuo08Artesanos y operarios de oficios -76.17
## ciuo08Operadores de instalaciones, maquinas y ensambladores -66.32
## ciuo08Ocupaciones elementales -84.60
## ciuo08Otros no identificados -17.48
## ciuo08Sin clasificación -14.71
## Pr(>|t|)
## (Intercept) <2e-16
## ciuo08Profesionales, científicos e intelectuales <2e-16
## ciuo08Técnicos y profesionales de nivel medio <2e-16
## ciuo08Personal de apoyo administrativo <2e-16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados <2e-16
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros <2e-16
## ciuo08Artesanos y operarios de oficios <2e-16
## ciuo08Operadores de instalaciones, maquinas y ensambladores <2e-16
## ciuo08Ocupaciones elementales <2e-16
## ciuo08Otros no identificados <2e-16
## ciuo08Sin clasificación <2e-16
##
## (Intercept) ***
## ciuo08Profesionales, científicos e intelectuales ***
## ciuo08Técnicos y profesionales de nivel medio ***
## ciuo08Personal de apoyo administrativo ***
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados ***
## ciuo08Sin clasificación ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10600000 on 26814 degrees of freedom
## (45110 observations deleted due to missingness)
## Multiple R-squared: 0.3095, Adjusted R-squared: 0.3092
## F-statistic: 1202 on 10 and 26814 DF, p-value: < 2.2e-16
Modelo para est_conyugal
modelo4 <- lm(ing_t_t ~ est_conyugal,
data = datos,
weights = fact_cal_esi)
summary(modelo4)
##
## Call:
## lm(formula = ing_t_t ~ est_conyugal, data = datos, weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -34630072 -4193409 -2453049 492227 322927197
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 411851 3546 116.13 <2e-16 ***
## est_conyugalSin pareja -185302 4956 -37.39 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9845000 on 58830 degrees of freedom
## (13103 observations deleted due to missingness)
## Multiple R-squared: 0.02321, Adjusted R-squared: 0.0232
## F-statistic: 1398 on 1 and 58830 DF, p-value: < 2.2e-16
En síntesis, el nivel de referencia siempre será el level más bajo de cada variable. Por ello es fundamental asegurarnos de que los factores que generemos en el código de procesamiento sea correcto y se adecue a nuestros fines.
5.4 Regresión lineal múltiple
¡Incorporemos más variables con el signo más (+)!
modelo5 <- lm(ing_t_t ~ edad + sexo + ciuo08 + est_conyugal,
data = datos,
weights = fact_cal_esi)
summary(modelo5)
##
## Call:
## lm(formula = ing_t_t ~ edad + sexo + ciuo08 + est_conyugal, data = datos,
## weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -77029860 -3327667 -903696 1562319 261766339
##
## Coefficients:
## Estimate
## (Intercept) 1977240.3
## edad 3645.5
## sexoMujer -179308.4
## ciuo08Profesionales, científicos e intelectuales -838561.6
## ciuo08Técnicos y profesionales de nivel medio -1245145.4
## ciuo08Personal de apoyo administrativo -1467502.5
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -1600971.8
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -1752079.3
## ciuo08Artesanos y operarios de oficios -1675160.8
## ciuo08Operadores de instalaciones, maquinas y ensambladores -1578961.8
## ciuo08Ocupaciones elementales -1718318.8
## ciuo08Otros no identificados -1042107.7
## ciuo08Sin clasificación -1693602.6
## est_conyugalSin pareja -113981.1
## Std. Error
## (Intercept) 23485.6
## edad 290.2
## sexoMujer 7968.4
## ciuo08Profesionales, científicos e intelectuales 21117.6
## ciuo08Técnicos y profesionales de nivel medio 21664.4
## ciuo08Personal de apoyo administrativo 24391.5
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 20672.5
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 30256.0
## ciuo08Artesanos y operarios de oficios 21582.2
## ciuo08Operadores de instalaciones, maquinas y ensambladores 23049.0
## ciuo08Ocupaciones elementales 20781.6
## ciuo08Otros no identificados 57343.4
## ciuo08Sin clasificación 115936.4
## est_conyugalSin pareja 7609.8
## t value
## (Intercept) 84.19
## edad 12.56
## sexoMujer -22.50
## ciuo08Profesionales, científicos e intelectuales -39.71
## ciuo08Técnicos y profesionales de nivel medio -57.47
## ciuo08Personal de apoyo administrativo -60.16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -77.44
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -57.91
## ciuo08Artesanos y operarios de oficios -77.62
## ciuo08Operadores de instalaciones, maquinas y ensambladores -68.50
## ciuo08Ocupaciones elementales -82.69
## ciuo08Otros no identificados -18.17
## ciuo08Sin clasificación -14.61
## est_conyugalSin pareja -14.98
## Pr(>|t|)
## (Intercept) <2e-16
## edad <2e-16
## sexoMujer <2e-16
## ciuo08Profesionales, científicos e intelectuales <2e-16
## ciuo08Técnicos y profesionales de nivel medio <2e-16
## ciuo08Personal de apoyo administrativo <2e-16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados <2e-16
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros <2e-16
## ciuo08Artesanos y operarios de oficios <2e-16
## ciuo08Operadores de instalaciones, maquinas y ensambladores <2e-16
## ciuo08Ocupaciones elementales <2e-16
## ciuo08Otros no identificados <2e-16
## ciuo08Sin clasificación <2e-16
## est_conyugalSin pareja <2e-16
##
## (Intercept) ***
## edad ***
## sexoMujer ***
## ciuo08Profesionales, científicos e intelectuales ***
## ciuo08Técnicos y profesionales de nivel medio ***
## ciuo08Personal de apoyo administrativo ***
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados ***
## ciuo08Sin clasificación ***
## est_conyugalSin pareja ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10400000 on 26807 degrees of freedom
## (45114 observations deleted due to missingness)
## Multiple R-squared: 0.3351, Adjusted R-squared: 0.3348
## F-statistic: 1039 on 13 and 26807 DF, p-value: < 2.2e-16
Regresión con paquete
stats tiene su función para generar diversos tipo de regresiones. Esta función es glm(), y tiene una estructura similar a lm(), sólo que en esta se debe especificar el tipo de regresión que se necesita en el argumento family. Así quedaría nuestro modelo de regresión lineal:
modelo5_glm <- glm(ing_t_t ~ edad + sexo + ciuo08 + est_conyugal,
family = gaussian(link = "identity"), #Especificamos la regresión lineal
data = datos,
weights = fact_cal_esi)
summary(modelo5_glm)
##
## Call:
## glm(formula = ing_t_t ~ edad + sexo + ciuo08 + est_conyugal,
## family = gaussian(link = "identity"), data = datos, weights = fact_cal_esi)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -77029860 -3327667 -903696 1562319 261766339
##
## Coefficients:
## Estimate
## (Intercept) 1977240.3
## edad 3645.5
## sexoMujer -179308.4
## ciuo08Profesionales, científicos e intelectuales -838561.6
## ciuo08Técnicos y profesionales de nivel medio -1245145.4
## ciuo08Personal de apoyo administrativo -1467502.5
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -1600971.8
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -1752079.3
## ciuo08Artesanos y operarios de oficios -1675160.8
## ciuo08Operadores de instalaciones, maquinas y ensambladores -1578961.8
## ciuo08Ocupaciones elementales -1718318.8
## ciuo08Otros no identificados -1042107.7
## ciuo08Sin clasificación -1693602.6
## est_conyugalSin pareja -113981.1
## Std. Error
## (Intercept) 23485.6
## edad 290.2
## sexoMujer 7968.4
## ciuo08Profesionales, científicos e intelectuales 21117.6
## ciuo08Técnicos y profesionales de nivel medio 21664.4
## ciuo08Personal de apoyo administrativo 24391.5
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 20672.5
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 30256.0
## ciuo08Artesanos y operarios de oficios 21582.2
## ciuo08Operadores de instalaciones, maquinas y ensambladores 23049.0
## ciuo08Ocupaciones elementales 20781.6
## ciuo08Otros no identificados 57343.4
## ciuo08Sin clasificación 115936.4
## est_conyugalSin pareja 7609.8
## t value
## (Intercept) 84.19
## edad 12.56
## sexoMujer -22.50
## ciuo08Profesionales, científicos e intelectuales -39.71
## ciuo08Técnicos y profesionales de nivel medio -57.47
## ciuo08Personal de apoyo administrativo -60.16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -77.44
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -57.91
## ciuo08Artesanos y operarios de oficios -77.62
## ciuo08Operadores de instalaciones, maquinas y ensambladores -68.50
## ciuo08Ocupaciones elementales -82.69
## ciuo08Otros no identificados -18.17
## ciuo08Sin clasificación -14.61
## est_conyugalSin pareja -14.98
## Pr(>|t|)
## (Intercept) <2e-16
## edad <2e-16
## sexoMujer <2e-16
## ciuo08Profesionales, científicos e intelectuales <2e-16
## ciuo08Técnicos y profesionales de nivel medio <2e-16
## ciuo08Personal de apoyo administrativo <2e-16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados <2e-16
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros <2e-16
## ciuo08Artesanos y operarios de oficios <2e-16
## ciuo08Operadores de instalaciones, maquinas y ensambladores <2e-16
## ciuo08Ocupaciones elementales <2e-16
## ciuo08Otros no identificados <2e-16
## ciuo08Sin clasificación <2e-16
## est_conyugalSin pareja <2e-16
##
## (Intercept) ***
## edad ***
## sexoMujer ***
## ciuo08Profesionales, científicos e intelectuales ***
## ciuo08Técnicos y profesionales de nivel medio ***
## ciuo08Personal de apoyo administrativo ***
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados ***
## ciuo08Sin clasificación ***
## est_conyugalSin pareja ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 1.08223e+14)
##
## Null deviance: 4.3633e+18 on 26820 degrees of freedom
## Residual deviance: 2.9011e+18 on 26807 degrees of freedom
## (45114 observations deleted due to missingness)
## AIC: 801135
##
## Number of Fisher Scoring iterations: 2
Regresión con paquete survey
survey también tiene su función para regresiones, para ello primero crearemos un objeto encuesta
esi_design <- as_survey_design(datos,
ids = 1,
weights = fact_cal_esi)
Luego usamos la función svyglm y en el argumento design dejamos el objeto creado y así generamos nuestro modelo:
modelo5_survey <- svyglm(ing_t_t ~ edad + sexo + ciuo08 + est_conyugal,
family = gaussian(link = "identity"),
design = esi_design)
Ahora visualizamos
summary(modelo5_survey)
##
## Call:
## svyglm(formula = ing_t_t ~ edad + sexo + ciuo08 + est_conyugal,
## design = esi_design, family = gaussian(link = "identity"))
##
## Survey design:
## Called via srvyr
##
## Coefficients:
## Estimate
## (Intercept) 1977240.3
## edad 3645.5
## sexoMujer -179308.4
## ciuo08Profesionales, científicos e intelectuales -838561.6
## ciuo08Técnicos y profesionales de nivel medio -1245145.4
## ciuo08Personal de apoyo administrativo -1467502.5
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -1600971.8
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -1752079.3
## ciuo08Artesanos y operarios de oficios -1675160.8
## ciuo08Operadores de instalaciones, maquinas y ensambladores -1578961.8
## ciuo08Ocupaciones elementales -1718318.8
## ciuo08Otros no identificados -1042107.7
## ciuo08Sin clasificación -1693602.6
## est_conyugalSin pareja -113981.1
## Std. Error
## (Intercept) 88363.0
## edad 452.1
## sexoMujer 13546.1
## ciuo08Profesionales, científicos e intelectuales 86714.7
## ciuo08Técnicos y profesionales de nivel medio 85675.3
## ciuo08Personal de apoyo administrativo 84472.8
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 83698.5
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 83437.6
## ciuo08Artesanos y operarios de oficios 83301.6
## ciuo08Operadores de instalaciones, maquinas y ensambladores 83666.1
## ciuo08Ocupaciones elementales 83108.3
## ciuo08Otros no identificados 103555.4
## ciuo08Sin clasificación 118605.3
## est_conyugalSin pareja 11951.0
## t value
## (Intercept) 22.376
## edad 8.063
## sexoMujer -13.237
## ciuo08Profesionales, científicos e intelectuales -9.670
## ciuo08Técnicos y profesionales de nivel medio -14.533
## ciuo08Personal de apoyo administrativo -17.372
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -19.128
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -20.999
## ciuo08Artesanos y operarios de oficios -20.110
## ciuo08Operadores de instalaciones, maquinas y ensambladores -18.872
## ciuo08Ocupaciones elementales -20.676
## ciuo08Otros no identificados -10.063
## ciuo08Sin clasificación -14.279
## est_conyugalSin pareja -9.537
## Pr(>|t|)
## (Intercept) < 2e-16
## edad 7.74e-16
## sexoMujer < 2e-16
## ciuo08Profesionales, científicos e intelectuales < 2e-16
## ciuo08Técnicos y profesionales de nivel medio < 2e-16
## ciuo08Personal de apoyo administrativo < 2e-16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados < 2e-16
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros < 2e-16
## ciuo08Artesanos y operarios de oficios < 2e-16
## ciuo08Operadores de instalaciones, maquinas y ensambladores < 2e-16
## ciuo08Ocupaciones elementales < 2e-16
## ciuo08Otros no identificados < 2e-16
## ciuo08Sin clasificación < 2e-16
## est_conyugalSin pareja < 2e-16
##
## (Intercept) ***
## edad ***
## sexoMujer ***
## ciuo08Profesionales, científicos e intelectuales ***
## ciuo08Técnicos y profesionales de nivel medio ***
## ciuo08Personal de apoyo administrativo ***
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados ***
## ciuo08Sin clasificación ***
## est_conyugalSin pareja ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 398202555644)
##
## Number of Fisher Scoring iterations: 2
Modelos de regresión logística
5.4 Información de los modelos
Para conocer la información de los modelos, hay múltiples funciones que podemos utilizar:
La primera función es str, la cual nos mostrará su estructura
str(modelo5)
## List of 15
## $ coefficients : Named num [1:14] 1977240 3645 -179308 -838562 -1245145 ...
## ..- attr(*, "names")= chr [1:14] "(Intercept)" "edad" "sexoMujer" "ciuo08Profesionales, científicos e intelectuales" ...
## $ residuals : Named num [1:26821] 17742 -204754 -102145 15920 -253034 ...
## ..- attr(*, "label")= chr "Total ingresos del trabajo"
## ..- attr(*, "format.stata")= chr "%10.0g"
## ..- attr(*, "names")= chr [1:26821] "1" "2" "3" "7" ...
## $ fitted.values: Named num [1:26821] 302679 954754 1002145 235781 393816 ...
## ..- attr(*, "label")= chr "Total ingresos del trabajo"
## ..- attr(*, "format.stata")= chr "%10.0g"
## ..- attr(*, "names")= chr [1:26821] "1" "2" "3" "7" ...
## $ effects : Named num [1:26821] -1.74e+09 1.33e+08 1.76e+08 6.89e+08 2.83e+08 ...
## ..- attr(*, "label")= chr "Total ingresos del trabajo"
## ..- attr(*, "format.stata")= chr "%10.0g"
## ..- attr(*, "names")= chr [1:26821] "(Intercept)" "edad" "sexoMujer" "ciuo08Profesionales, científicos e intelectuales" ...
## $ weights : num [1:26821] 345.8 1056.5 41.6 730.4 270.1 ...
## $ rank : int 14
## $ assign : int [1:14] 0 1 2 3 3 3 3 3 3 3 ...
## $ qr :List of 5
## ..$ qr : num [1:26821, 1:14] -2.84e+03 1.15e-02 2.27e-03 9.52e-03 5.79e-03 ...
## .. ..- attr(*, "assign")= int [1:14] 0 1 2 3 3 3 3 3 3 3 ...
## .. ..- attr(*, "contrasts")=List of 3
## .. .. ..$ sexo : chr "contr.treatment"
## .. .. ..$ ciuo08 : chr "contr.treatment"
## .. .. ..$ est_conyugal: chr "contr.treatment"
## .. ..- attr(*, "dimnames")=List of 2
## .. .. ..$ : chr [1:26821] "1" "2" "3" "7" ...
## .. .. ..$ : chr [1:14] "(Intercept)" "edad" "sexoMujer" "ciuo08Profesionales, científicos e intelectuales" ...
## ..$ qraux: num [1:14] 1.01 1.01 1 1.01 1 ...
## ..$ pivot: int [1:14] 1 2 3 4 5 6 7 8 9 10 ...
## ..$ tol : num 1e-07
## ..$ rank : int 14
## ..- attr(*, "class")= chr "qr"
## $ df.residual : int 26807
## $ na.action : 'omit' Named int [1:45114] 4 5 6 8 11 14 16 17 19 21 ...
## ..- attr(*, "names")= chr [1:45114] "4" "5" "6" "8" ...
## $ contrasts :List of 3
## ..$ sexo : chr "contr.treatment"
## ..$ ciuo08 : chr "contr.treatment"
## ..$ est_conyugal: chr "contr.treatment"
## $ xlevels :List of 3
## ..$ sexo : chr [1:2] "Hombre" "Mujer"
## ..$ ciuo08 : chr [1:11] "Directores, gerentes y administradores" "Profesionales, científicos e intelectuales" "Técnicos y profesionales de nivel medio" "Personal de apoyo administrativo" ...
## ..$ est_conyugal: chr [1:2] "Con pareja" "Sin pareja"
## $ call : language lm(formula = ing_t_t ~ edad + sexo + ciuo08 + est_conyugal, data = datos, weights = fact_cal_esi)
## $ terms :Classes 'terms', 'formula' language ing_t_t ~ edad + sexo + ciuo08 + est_conyugal
## .. ..- attr(*, "variables")= language list(ing_t_t, edad, sexo, ciuo08, est_conyugal)
## .. ..- attr(*, "factors")= int [1:5, 1:4] 0 1 0 0 0 0 0 1 0 0 ...
## .. .. ..- attr(*, "dimnames")=List of 2
## .. .. .. ..$ : chr [1:5] "ing_t_t" "edad" "sexo" "ciuo08" ...
## .. .. .. ..$ : chr [1:4] "edad" "sexo" "ciuo08" "est_conyugal"
## .. ..- attr(*, "term.labels")= chr [1:4] "edad" "sexo" "ciuo08" "est_conyugal"
## .. ..- attr(*, "order")= int [1:4] 1 1 1 1
## .. ..- attr(*, "intercept")= int 1
## .. ..- attr(*, "response")= int 1
## .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. ..- attr(*, "predvars")= language list(ing_t_t, edad, sexo, ciuo08, est_conyugal)
## .. ..- attr(*, "dataClasses")= Named chr [1:6] "numeric" "numeric" "factor" "factor" ...
## .. .. ..- attr(*, "names")= chr [1:6] "ing_t_t" "edad" "sexo" "ciuo08" ...
## $ model :'data.frame': 26821 obs. of 6 variables:
## ..$ ing_t_t : num [1:26821] 320421 750000 900000 251701 140782 ...
## .. ..- attr(*, "label")= chr "Total ingresos del trabajo"
## .. ..- attr(*, "format.stata")= chr "%10.0g"
## ..$ edad : num [1:26821] 29 30 43 31 54 67 50 43 59 40 ...
## .. ..- attr(*, "label")= chr "Edad de la persona"
## .. ..- attr(*, "format.stata")= chr "%10.0g"
## ..$ sexo : Factor w/ 2 levels "Hombre","Mujer": 2 2 2 2 2 2 1 2 1 2 ...
## .. ..- attr(*, "label")= chr "Sexo"
## ..$ ciuo08 : Factor w/ 11 levels "Directores, gerentes y administradores",..: 5 2 2 7 5 9 4 4 8 5 ...
## .. ..- attr(*, "label")= chr "b1. Grupo ocupacional según CIUO 08 - 1 dígito"
## ..$ est_conyugal: Factor w/ 2 levels "Con pareja","Sin pareja": 1 2 2 1 1 1 1 2 1 2 ...
## ..$ (weights) : num [1:26821] 345.8 1056.5 41.6 730.4 270.1 ...
## .. ..- attr(*, "label")= chr "Factor de expansión ESI con nueva calibración, proyecciones de población "
## .. ..- attr(*, "format.stata")= chr "%10.0g"
## ..- attr(*, "terms")=Classes 'terms', 'formula' language ing_t_t ~ edad + sexo + ciuo08 + est_conyugal
## .. .. ..- attr(*, "variables")= language list(ing_t_t, edad, sexo, ciuo08, est_conyugal)
## .. .. ..- attr(*, "factors")= int [1:5, 1:4] 0 1 0 0 0 0 0 1 0 0 ...
## .. .. .. ..- attr(*, "dimnames")=List of 2
## .. .. .. .. ..$ : chr [1:5] "ing_t_t" "edad" "sexo" "ciuo08" ...
## .. .. .. .. ..$ : chr [1:4] "edad" "sexo" "ciuo08" "est_conyugal"
## .. .. ..- attr(*, "term.labels")= chr [1:4] "edad" "sexo" "ciuo08" "est_conyugal"
## .. .. ..- attr(*, "order")= int [1:4] 1 1 1 1
## .. .. ..- attr(*, "intercept")= int 1
## .. .. ..- attr(*, "response")= int 1
## .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. .. ..- attr(*, "predvars")= language list(ing_t_t, edad, sexo, ciuo08, est_conyugal)
## .. .. ..- attr(*, "dataClasses")= Named chr [1:6] "numeric" "numeric" "factor" "factor" ...
## .. .. .. ..- attr(*, "names")= chr [1:6] "ing_t_t" "edad" "sexo" "ciuo08" ...
## ..- attr(*, "na.action")= 'omit' Named int [1:45114] 4 5 6 8 11 14 16 17 19 21 ...
## .. ..- attr(*, "names")= chr [1:45114] "4" "5" "6" "8" ...
## - attr(*, "class")= chr "lm"
Luego esta summary, la cual hemos estado utilizando a lo largo del práctico
summary(modelo5)
##
## Call:
## lm(formula = ing_t_t ~ edad + sexo + ciuo08 + est_conyugal, data = datos,
## weights = fact_cal_esi)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -77029860 -3327667 -903696 1562319 261766339
##
## Coefficients:
## Estimate
## (Intercept) 1977240.3
## edad 3645.5
## sexoMujer -179308.4
## ciuo08Profesionales, científicos e intelectuales -838561.6
## ciuo08Técnicos y profesionales de nivel medio -1245145.4
## ciuo08Personal de apoyo administrativo -1467502.5
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -1600971.8
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -1752079.3
## ciuo08Artesanos y operarios de oficios -1675160.8
## ciuo08Operadores de instalaciones, maquinas y ensambladores -1578961.8
## ciuo08Ocupaciones elementales -1718318.8
## ciuo08Otros no identificados -1042107.7
## ciuo08Sin clasificación -1693602.6
## est_conyugalSin pareja -113981.1
## Std. Error
## (Intercept) 23485.6
## edad 290.2
## sexoMujer 7968.4
## ciuo08Profesionales, científicos e intelectuales 21117.6
## ciuo08Técnicos y profesionales de nivel medio 21664.4
## ciuo08Personal de apoyo administrativo 24391.5
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 20672.5
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 30256.0
## ciuo08Artesanos y operarios de oficios 21582.2
## ciuo08Operadores de instalaciones, maquinas y ensambladores 23049.0
## ciuo08Ocupaciones elementales 20781.6
## ciuo08Otros no identificados 57343.4
## ciuo08Sin clasificación 115936.4
## est_conyugalSin pareja 7609.8
## t value
## (Intercept) 84.19
## edad 12.56
## sexoMujer -22.50
## ciuo08Profesionales, científicos e intelectuales -39.71
## ciuo08Técnicos y profesionales de nivel medio -57.47
## ciuo08Personal de apoyo administrativo -60.16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -77.44
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -57.91
## ciuo08Artesanos y operarios de oficios -77.62
## ciuo08Operadores de instalaciones, maquinas y ensambladores -68.50
## ciuo08Ocupaciones elementales -82.69
## ciuo08Otros no identificados -18.17
## ciuo08Sin clasificación -14.61
## est_conyugalSin pareja -14.98
## Pr(>|t|)
## (Intercept) <2e-16
## edad <2e-16
## sexoMujer <2e-16
## ciuo08Profesionales, científicos e intelectuales <2e-16
## ciuo08Técnicos y profesionales de nivel medio <2e-16
## ciuo08Personal de apoyo administrativo <2e-16
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados <2e-16
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros <2e-16
## ciuo08Artesanos y operarios de oficios <2e-16
## ciuo08Operadores de instalaciones, maquinas y ensambladores <2e-16
## ciuo08Ocupaciones elementales <2e-16
## ciuo08Otros no identificados <2e-16
## ciuo08Sin clasificación <2e-16
## est_conyugalSin pareja <2e-16
##
## (Intercept) ***
## edad ***
## sexoMujer ***
## ciuo08Profesionales, científicos e intelectuales ***
## ciuo08Técnicos y profesionales de nivel medio ***
## ciuo08Personal de apoyo administrativo ***
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados ***
## ciuo08Sin clasificación ***
## est_conyugalSin pareja ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10400000 on 26807 degrees of freedom
## (45114 observations deleted due to missingness)
## Multiple R-squared: 0.3351, Adjusted R-squared: 0.3348
## F-statistic: 1039 on 13 and 26807 DF, p-value: < 2.2e-16
¿Pero que pasa si queremos un elemento en particular del modelo?, como este es un objeto, se puede utilizar el símbolo $ para extraer información de este
modelo5$coefficients
## (Intercept)
## 1977240.278
## edad
## 3645.488
## sexoMujer
## -179308.422
## ciuo08Profesionales, científicos e intelectuales
## -838561.638
## ciuo08Técnicos y profesionales de nivel medio
## -1245145.411
## ciuo08Personal de apoyo administrativo
## -1467502.547
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados
## -1600971.794
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros
## -1752079.303
## ciuo08Artesanos y operarios de oficios
## -1675160.786
## ciuo08Operadores de instalaciones, maquinas y ensambladores
## -1578961.831
## ciuo08Ocupaciones elementales
## -1718318.836
## ciuo08Otros no identificados
## -1042107.683
## ciuo08Sin clasificación
## -1693602.555
## est_conyugalSin pareja
## -113981.138
modelo5$coefficients[2]
## edad
## 3645.488
modelo5$coefficients["edad"]
## edad
## 3645.488
¿Qué otros elementos puedo extraer?, para eso str nos dirá estructura y elementos que podremos utilizar
str(summary(modelo5))
## List of 13
## $ call : language lm(formula = ing_t_t ~ edad + sexo + ciuo08 + est_conyugal, data = datos, weights = fact_cal_esi)
## $ terms :Classes 'terms', 'formula' language ing_t_t ~ edad + sexo + ciuo08 + est_conyugal
## .. ..- attr(*, "variables")= language list(ing_t_t, edad, sexo, ciuo08, est_conyugal)
## .. ..- attr(*, "factors")= int [1:5, 1:4] 0 1 0 0 0 0 0 1 0 0 ...
## .. .. ..- attr(*, "dimnames")=List of 2
## .. .. .. ..$ : chr [1:5] "ing_t_t" "edad" "sexo" "ciuo08" ...
## .. .. .. ..$ : chr [1:4] "edad" "sexo" "ciuo08" "est_conyugal"
## .. ..- attr(*, "term.labels")= chr [1:4] "edad" "sexo" "ciuo08" "est_conyugal"
## .. ..- attr(*, "order")= int [1:4] 1 1 1 1
## .. ..- attr(*, "intercept")= int 1
## .. ..- attr(*, "response")= int 1
## .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
## .. ..- attr(*, "predvars")= language list(ing_t_t, edad, sexo, ciuo08, est_conyugal)
## .. ..- attr(*, "dataClasses")= Named chr [1:6] "numeric" "numeric" "factor" "factor" ...
## .. .. ..- attr(*, "names")= chr [1:6] "ing_t_t" "edad" "sexo" "ciuo08" ...
## $ weights : num [1:26821] 345.8 1056.5 41.6 730.4 270.1 ...
## $ residuals : Named num [1:26821] 329915 -6655171 -658927 430264 -4158305 ...
## ..- attr(*, "label")= chr "Total ingresos del trabajo"
## ..- attr(*, "format.stata")= chr "%10.0g"
## ..- attr(*, "names")= chr [1:26821] "1" "2" "3" "7" ...
## $ coefficients : num [1:14, 1:4] 1977240 3645 -179308 -838562 -1245145 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:14] "(Intercept)" "edad" "sexoMujer" "ciuo08Profesionales, científicos e intelectuales" ...
## .. ..$ : chr [1:4] "Estimate" "Std. Error" "t value" "Pr(>|t|)"
## $ aliased : Named logi [1:14] FALSE FALSE FALSE FALSE FALSE FALSE ...
## ..- attr(*, "names")= chr [1:14] "(Intercept)" "edad" "sexoMujer" "ciuo08Profesionales, científicos e intelectuales" ...
## $ sigma : num 10403029
## $ df : int [1:3] 14 26807 14
## $ r.squared : num 0.335
## $ adj.r.squared: num 0.335
## $ fstatistic : Named num [1:3] 1039 13 26807
## ..- attr(*, "names")= chr [1:3] "value" "numdf" "dendf"
## $ cov.unscaled : num [1:14, 1:14] 5.10e-06 -3.68e-08 -1.59e-07 -3.41e-06 -3.38e-06 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:14] "(Intercept)" "edad" "sexoMujer" "ciuo08Profesionales, científicos e intelectuales" ...
## .. ..$ : chr [1:14] "(Intercept)" "edad" "sexoMujer" "ciuo08Profesionales, científicos e intelectuales" ...
## $ na.action : 'omit' Named int [1:45114] 4 5 6 8 11 14 16 17 19 21 ...
## ..- attr(*, "names")= chr [1:45114] "4" "5" "6" "8" ...
## - attr(*, "class")= chr "summary.lm"
summary(modelo5)$fstatistic
## value numdf dendf
## 1039.257 13.000 26807.000
summary(modelo5)$r.squared
## [1] 0.3351
Para los valores predichos utilizaremos la función de sjPlot::get_model_data()
modelo5$fitted.values
get_model_data(modelo5,
type = "pred")
## $edad
## # Predicted values of Total ingresos del trabajo
##
## edad | Predicted | group_col | 95% CI
## ---------------------------------------------------
## 10 | 2.01e+06 | edad | [1.97e+06, 2.06e+06]
## 20 | 2.05e+06 | edad | [2.01e+06, 2.09e+06]
## 30 | 2.09e+06 | edad | [2.05e+06, 2.13e+06]
## 40 | 2.12e+06 | edad | [2.09e+06, 2.16e+06]
## 60 | 2.20e+06 | edad | [2.16e+06, 2.23e+06]
## 70 | 2.23e+06 | edad | [2.19e+06, 2.27e+06]
## 80 | 2.27e+06 | edad | [2.23e+06, 2.31e+06]
## 100 | 2.34e+06 | edad | [2.29e+06, 2.39e+06]
##
## Adjusted for:
## * sexo = Hombre
## * ciuo08 = Directores, gerentes y administradores
## * est_conyugal = Con pareja
##
## $sexo
## # Predicted values of Total ingresos del trabajo
##
## sexo | Predicted | group_col | 95% CI
## ---------------------------------------------------
## 1 | 2.13e+06 | sexo | [2.09e+06, 2.17e+06]
## 2 | 1.95e+06 | sexo | [1.91e+06, 1.99e+06]
##
## Adjusted for:
## * edad = 42.13
## * ciuo08 = Directores, gerentes y administradores
## * est_conyugal = Con pareja
##
## $ciuo08
## # Predicted values of Total ingresos del trabajo
##
## ciuo08 | Predicted | group_col | 95% CI
## -----------------------------------------------------
## 1 | 2.13e+06 | ciuo08 | [2.09e+06, 2.17e+06]
## 2 | 1.29e+06 | ciuo08 | [1.27e+06, 1.31e+06]
## 4 | 6.63e+05 | ciuo08 | [6.32e+05, 6.95e+05]
## 5 | 5.30e+05 | ciuo08 | [5.11e+05, 5.49e+05]
## 6 | 3.79e+05 | ciuo08 | [3.32e+05, 4.26e+05]
## 7 | 4.56e+05 | ciuo08 | [4.34e+05, 4.77e+05]
## 8 | 5.52e+05 | ciuo08 | [5.26e+05, 5.78e+05]
## 11 | 4.37e+05 | ciuo08 | [2.13e+05, 6.61e+05]
##
## Adjusted for:
## * edad = 42.13
## * sexo = Hombre
## * est_conyugal = Con pareja
##
## $est_conyugal
## # Predicted values of Total ingresos del trabajo
##
## est_conyugal | Predicted | group_col | 95% CI
## --------------------------------------------------------------
## 1 | 2.13e+06 | est_conyugal | [2.09e+06, 2.17e+06]
## 2 | 2.02e+06 | est_conyugal | [1.98e+06, 2.06e+06]
##
## Adjusted for:
## * edad = 42.13
## * sexo = Hombre
## * ciuo08 = Directores, gerentes y administradores
get_model_data(modelo5,
type = "pred",
terms = "sexo")
## # Predicted values of Total ingresos del trabajo
##
## sexo | Predicted | group_col | 95% CI
## ---------------------------------------------------
## 1 | 2.13e+06 | 1 | [2.09e+06, 2.17e+06]
## 2 | 1.95e+06 | 1 | [1.91e+06, 1.99e+06]
##
## Adjusted for:
## * edad = 42.13
## * ciuo08 = Directores, gerentes y administradores
## * est_conyugal = Con pareja
BONUS
Con broom, podemos convertir objetos en dataframes, lo cual nos permitirá presentarlo con tab_df de sjPlot
print <- broom::augment(modelo5)
tab_df(print, file = "output/data/modelo.doc")
Esto nos lleva al último punto del práctico, la visualización
6. Visualización
Si bien summary es un código muy útil para visualizar los modelos creados, el problema es que al observar el objeto creado, no es muy presentable para informes, por eso usaremos la función tab_model de sjPlot, que tiene la siguiente estructura:
sjPlot::tab_model(objeto_creado,
show.ci= F/T, # este argumento muestra los intervalos de confianza
show.p = F/T, #Este argumento muestra los valores p
show.obs = F/T, # Este argumento muestra las observaciones
title = "Título de la tabla a crear",
digits = 2, # muestra la cantidad de dígitos que tednrá la tabla
p.style = c("numeric", "stars", "numeric_stars", "scientific", "scientific_stars"), #cómo representa el pvalue
encoding = "UTF-8", # evita errores en caracteres
file = "output/figures/reg1_tab.doc") # guarda lo creado automáticamente
Para visualizar sólo un modelo puede hacerse de esta forma y en nuestros datos se vería así:
sjPlot::tab_model(modelo0,
show.ci=FALSE,
encoding = "UTF-8",
file = "output/figures/regnc_tab.doc")
| Total ingresos del trabajo |
||
|---|---|---|
| Predictors | Estimates | p |
| (Intercept) | 256201.13 | <0.001 |
| Observations | 71935 | |
| R2 / R2 adjusted | 0.000 / 0.000 | |
Las ventajas de este código es que se puede especificar el encoding, así como exportar la tabla, cuya presentación es superior al output de la función summary()
Pero además se pueden incluir más modelos creados en una sola tabla, para eso usaremos nuevamente la función tab_model de sjPlot
sjPlot::tab_model(list(modelo0, modelo1, modelo2), # los modelos estimados
show.ci=FALSE, # no mostrar intervalo de confianza (por defecto lo hace)
p.style = "stars", # asteriscos de significación estadística
dv.labels = c("Modelo 1", "Modelo 2", "Modelo 3"), # etiquetas de modelos o variables dep.
string.pred = "Predictores", string.est = "β", # nombre predictores y símbolo beta en tabla
encoding = "UTF-8",
file = "output/figures/reg_tab_all.doc")
| Modelo 1 | Modelo 2 | Modelo 3 | |
|---|---|---|---|
| Predictores | ß | ß | ß |
| (Intercept) | 256201.13 *** | 127658.05 *** | 337663.87 *** |
| Edad de la persona | 3511.38 *** | ||
| Sexo: Mujer | -160784.29 *** | ||
| Observations | 71935 | 71935 | 71935 |
| R2 / R2 adjusted | 0.000 / 0.000 | 0.019 / 0.019 | 0.021 / 0.021 |
| * p<0.05 ** p<0.01 *** p<0.001 | |||
También se pueden especificar las etiquetas con dv.labels y cómo queremos que nos incorpore la significación estadística, con p.style
Para visualizar o graficar los coeficientes de regresión para poder observar el impacto de cada variable en el modelo utilizaremos la función plot_model de sjPlot, su estructura es la siguiente:
sjPlot::plot_model(objeto_creado,
ci.lvl = "", #estima el nivel de confianza
title = "", # es el título
show.p = T, # nos muestra los valores p
show.values = T, # nos muestra los valores
vline.color = "") # color de la recta vertical
Esto visualizado con nuestro modelo se ve así:
sjPlot::plot_model(modelo5,
show.p = T,
show.values = T,
ci.lvl = c(0.95),
title = "Estimación de predictores",
vline.color = "purple")
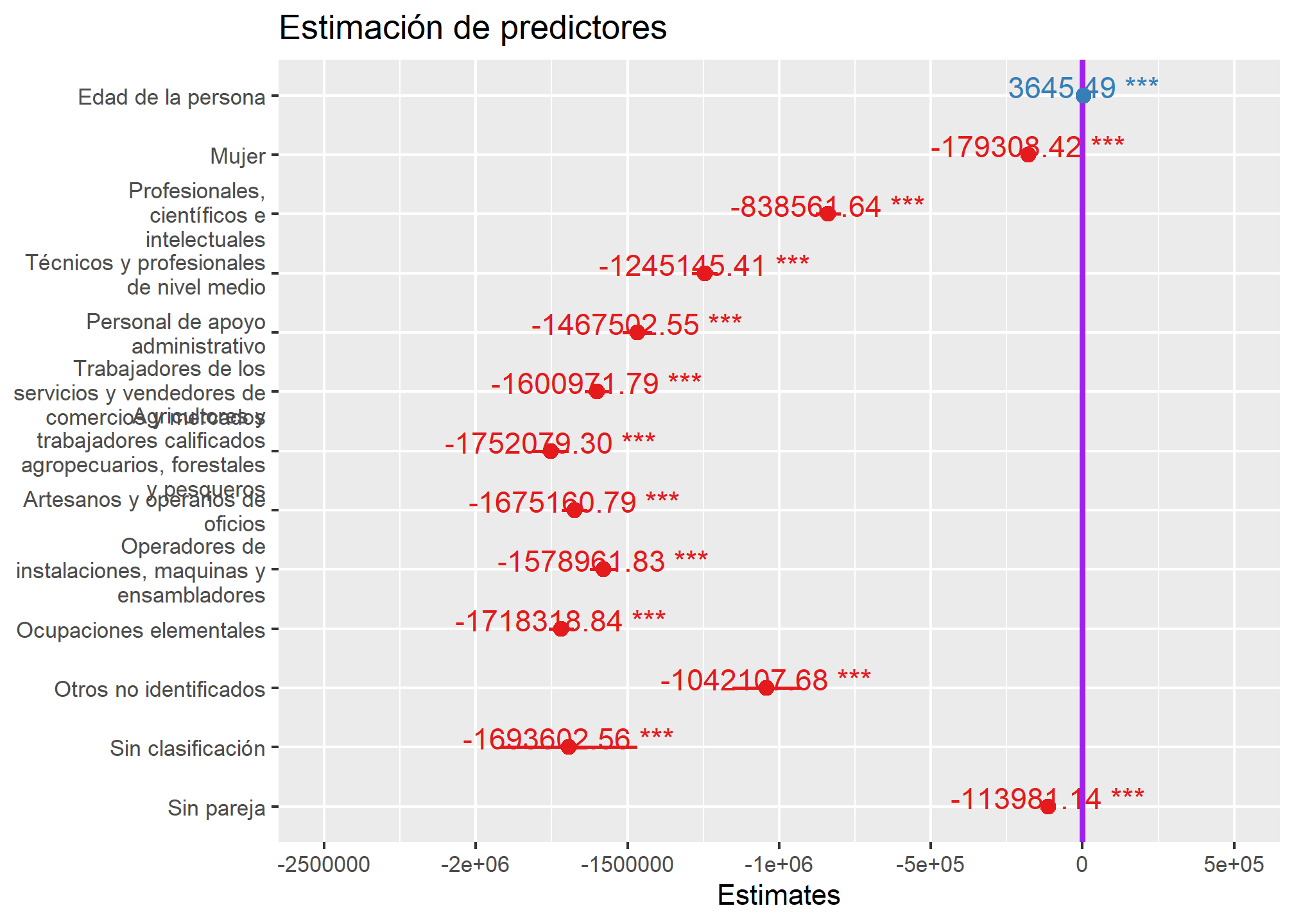
Terminamos por este práctico ¡Pero aún falta la regresión logística!, para eso nos vemos en la próxima clase
7. Resumen
En este práctico aprendimos a
- Crear y visualizar regresiones lineales y logísticas binomiales
- Incorporar predictores categóricos
- Crear y visualizar regresiones múltiples