Regresión logística
0. Objetivos del práctico
Este práctico tiene por objetivo presentar cómo crear modelos de regresión logística - con y sin consideración de diseño muestral - en R, con predictores categóricos y cuantitativos; cómo exponenciar los coeficientes para facilitar su interpretación; y, por último, herramientas de visualización de los modelos generados (sobre todo con texreg). Por supuesto, seguimos en el proceso de análisis de datos

1. Recursos del práctico
Este práctico fue elaborado con datos de la Encuesta Suplementaria de Ingresos (ESI) en su versión 2020. Cuando trabajen con algún set de datos, nunca olviden revisar la documentación metodológica anexa, así como el libro de códigos correspondiente.
Los datos ya fueron procesados anteriormente, a modo de concentrar el práctico en la creación de los modelos. Así, por ejemplo, los predictores categóricos ya fueron transformados en variables de tipo factor. Pueden revisar el script proc.R ubicado en la carpeta R, para profundizar en el tratamiento de los datos.
2. Librerías a utilizar
En este práctico utilizaremos seis paquetes
-
pacman: este facilita y agiliza la lectura de los paquetes a utilizar en R; -
tidyverse: colección de paquetes; -
srvyr: para crear el objeto encuesta; -
survey: para crear modelos incorporando el diseño muestral; -
sjPlot: para presentar tablas y gráficos con los modelos creados; -
remotes: para instalartexregdesde GitHub; -
texreg: para crear tablas en formato publicable.
Pasos del procesamiento
1. Cargar librerías
Como en las prácticas anteriores, empleamos la función p_load de la librería pacman. También utilizamos la función install_github() de remotes para poder instalar la librería texreg
remotes::install_github("leifeld/texreg", force = T)
##
## * checking for file 'C:\Users\dafne\AppData\Local\Temp\RtmpaoqnDt\remotes4ec2e6490b\leifeld-texreg-a80fce7/DESCRIPTION' ... OK
## * preparing 'texreg':
## * checking DESCRIPTION meta-information ... OK
## * installing the package to process help pages
## * saving partial Rd database
## * checking for LF line-endings in source and make files and shell scripts
## * checking for empty or unneeded directories
## * building 'texreg_1.38.6.tar.gz'
##
pacman::p_load(sjPlot,
tidyverse,
srvyr,
survey,
remotes,
texreg)
2. Cargar datos
Como se señaló anteriormente, en este práctico se trabajará con los datos de la Encuesta Suplementaria de Ingresos (ESI) en su versión 2020. Esta se encuentra en la carpeta “input/data”, en formato .rds, habiendo sido procesada anteriormente. Por ello, empleamos la función readRDS() de la librería base de R.
datos <- readRDS(url("https://github.com/learn-R/10.2-class/raw/main/input/data/data_proc.rds"))
Podemos darnos cuenta de que el set de datos presenta 26.821 observaciones (o filas), y 7 variables (o columnas), que incluyen a las variables ing_t_t,, edad, sexo, est_conyugal, ciuo08, fact_cal_esi y ing_medio. Esta última discrimina si el sujeto presenta ingresos mayores o iguales (1) a la media de ing_t_t o no (0). Para mayor detalle, revisar el script proc.R ubicado en la carpeta R, para profundizar en el tratamiento de los datos.
3. Explorar datos
A continuación, usaremos la función view_df() del paquete sjPlot, que presenta un resumen de las variables contenidas en el set de datos, que nos permitirá identificar la etiqueta de cada variable y de cada una de sus alternativas de respuesta.
sjPlot::view_df(datos,
encoding = 'latin9')
| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | ing_t_t | Total ingresos del trabajo | range: 0.0-18045761.6 | |
| 2 | edad | Edad de la persona | range: 15-93 | |
| 3 | sexo | Sexo | Hombre Mujer |
|
| 4 | est_conyugal | Con pareja Sin pareja |
||
| 5 | ciuo08 | b1. Grupo ocupacional según CIUO 08 - 1 dÃgito | Directores, gerentes y administradores Profesionales, cientÃficos e intelectuales Técnicos y profesionales de nivel medio Personal de apoyo administrativo Trabajadores de los servicios y vendedores de comercios y mercados Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros Artesanos y operarios de oficios Operadores de instalaciones, maquinas y ensambladores Ocupaciones elementales Otros no identificados Sin clasificación |
|
| 6 | fact_cal_esi | Factor de expansión ESI con nueva calibración, proyecciones de población |
range: 6.7-7070.1 | |
| 7 | ing_medio | ¿Mayor que el ingreso medio? | 0 1 |
|
Podemos ver que tenemos tres variables cuantitativas (ing_t_t, edad y fact_cal_esi), y cuatro variables categóricas (sexo, est_conyugal, ciuo08 e ing_medio). Estas últimas tienen 2, 2, 10 y 2 categorías, respectivamente.
4. Creación del modelo de regresión logística binaria
La regresión logística binaria
Recordemos que, en el caso de la regresión logística, el resultado predicho es el logit (logatirmos de los odds), siendo los odds una razón de probabilidades (chances). Para llegar hasta la regresión logística, debemos pasar por los odds y los odds-ratio (proporción de chances).
Las odds son la probabilidad de que algo ocurra (por ejemplo, tener un ingreso mayor o igual a la media) dividido por la probabilidad de que no ocurra:
\begin{equation} \ Odds = p/1-p \end{equation}
Odds de 1 significan chances iguales, mientras que odds inferiores a 1 son negativas, y mayores a 1, positivas.
Las Odds ratio (OR), por su parte, reflejan la asociación entre las chances de dos variables dicotómicas:
\begin{equation} \ OR = p_1/(1-p_1)/p_0/(1-p_0) \end{equation}
Las OR permiten, entonces, presentar en un único número la relación entre dos variables categóricas. Por ello, es una versión del β para variables dependientes categóricas. Una de las transformaciones que permite estimar una regresión con variables dependientes dicotómicas es el logit, logaritmo de los odds
\begin{equation} \ Logit = ln(Odd) = ln(p/1-p) \end{equation}
Luego, la fórmula para un modelo de regresión logística binaria simple es
\begin{equation} \ E(Y) = P = exp(b_{0} + b_{1}X) / 1 + exp(b_{0} + b_{1}X) \end{equation}
Donde
\(E(Y)\)es el valor estimado/predicho de\(Y\)\(P\)es la probabilidad predicha\(b_{0}\)es el intercepto\(b_{1}\)es el coeficiente de regresión que, en este caso, presenta valores en log-odds
Y para la regresión logística binaria múltiple
\begin{equation} \ E(Y) = P = exp(b_{0} + b_{1}X_{1} + b_{n}X_{n}) / 1 + exp(b_{0} + b_{1}X_{1} + b_{n}X_{n}) \end{equation}
Donde
\(E(Y)\)es el valor estimado/predicho de\(Y\)\(P\)es la probabilidad predicha\(b_{0}\)es el intercepto\(b_{1}\)es el coeficiente de regresión del primer predictor que, en este caso, presenta valores en log-odds\(b_{n}\)es el coeficiente de regresión del predictor n que, en este caso, presenta valores en log-odds
a) Modelo nulo
Una vez realizado lo anterior, es momento de generar nuestro modelo de regresión logística. Emplearemos la función glm() del paquete base de R, especificando el argumento family como "binomial". Lo primero es especificar las variables con las cuales construiremos el modelo: antes de la virgulilla (~) escribiremos nuestra variable dependiente (en este caso, ing_medio), y luego, las variables independientes separadas con un signo más (+). Para crear el modelo nulo, en lugar de variables predictoras, especificamos un 1. En síntesis, las diferencias entre crear un modelo de regresión lineal (como se revisó en el práctico anterior) son:
- Se utiliza la función
glm()en lugar delm() - Se especifica el argumento
family = 'binomial'
modelo0 <- glm(ing_medio ~ 1,
data = datos,
weights = fact_cal_esi,
family = binomial(link = "logit"))
Examinemos el modelo creado:
summary(modelo0)
##
## Call:
## glm(formula = ing_medio ~ 1, family = binomial(link = "logit"),
## data = datos, weights = fact_cal_esi)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -625.3 0.0 0.0 0.0 0.0
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1615045593563038 23644 68307515464 <0.0000000000000002
##
## (Intercept) ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 8361355 on 26820 degrees of freedom
## Residual deviance: 124161070 on 26820 degrees of freedom
## AIC: 124159719
##
## Number of Fisher Scoring iterations: 6
Como podemos ver, se ha creado en nuestro entorno (Environment) un objeto llamado modelo0_sin, que consta de una lista con 30 elementos.
b) Modelo con predictores numéricos
No obstante, el modelo nulo no es interpretable. Incorporemos edad, predictor numérico, y revisemos el modelo estimado
modelo1 <- glm(ing_medio ~ edad,
data = datos,
family = binomial(link = "logit"))
summary(modelo1)
##
## Call:
## glm(formula = ing_medio ~ edad, family = binomial(link = "logit"),
## data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7254 0.7211 0.7409 0.7576 0.8079
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.287250 0.048275 26.66 < 0.0000000000000002 ***
## edad -0.003642 0.001026 -3.55 0.000385 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 29882 on 26820 degrees of freedom
## Residual deviance: 29869 on 26819 degrees of freedom
## AIC: 29873
##
## Number of Fisher Scoring iterations: 4
c) Modelo con predictores categóricos
Asimismo, gran parte de las veces queremos utilizar variables categóricas (como el sexo, la ocupación o el estado conyugal de las personas) como variables predictoras:
modelo2 <- glm(ing_medio ~ sexo,
data = datos,
family = binomial(link = "logit"))
summary(modelo2)
##
## Call:
## glm(formula = ing_medio ~ sexo, family = binomial(link = "logit"),
## data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7766 0.6799 0.6799 0.8397 0.8397
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.34711 0.01996 67.48 <0.0000000000000002 ***
## sexoMujer -0.48607 0.02855 -17.03 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 29882 on 26820 degrees of freedom
## Residual deviance: 29592 on 26819 degrees of freedom
## AIC: 29596
##
## Number of Fisher Scoring iterations: 4
d) Modelo completo
¡Incorporemos todas las variables que seleccionamos!
modelo3 <- glm(ing_medio ~ edad + sexo + ciuo08 + est_conyugal,
data = datos,
family = binomial(link = "logit"))
summary(modelo3)
##
## Call:
## glm(formula = ing_medio ~ edad + sexo + ciuo08 + est_conyugal,
## family = binomial(link = "logit"), data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.59360 0.00095 0.50005 0.82422 1.34623
##
## Coefficients:
## Estimate
## (Intercept) 3.184303
## edad 0.002147
## sexoMujer -0.756990
## ciuo08Profesionales, científicos e intelectuales -0.040840
## ciuo08Técnicos y profesionales de nivel medio -0.344910
## ciuo08Personal de apoyo administrativo -0.439180
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -1.989663
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -2.695957
## ciuo08Artesanos y operarios de oficios -2.346364
## ciuo08Operadores de instalaciones, maquinas y ensambladores -1.273414
## ciuo08Ocupaciones elementales -2.208624
## ciuo08Otros no identificados 11.524044
## ciuo08Sin clasificación -2.460523
## est_conyugalSin pareja -0.167130
## Std. Error
## (Intercept) 0.165321
## edad 0.001101
## sexoMujer 0.033434
## ciuo08Profesionales, científicos e intelectuales 0.168604
## ciuo08Técnicos y profesionales de nivel medio 0.166762
## ciuo08Personal de apoyo administrativo 0.179496
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 0.156859
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 0.165042
## ciuo08Artesanos y operarios de oficios 0.158416
## ciuo08Operadores de instalaciones, maquinas y ensambladores 0.166563
## ciuo08Ocupaciones elementales 0.156421
## ciuo08Otros no identificados 70.479870
## ciuo08Sin clasificación 0.490312
## est_conyugalSin pareja 0.039472
## z value
## (Intercept) 19.261
## edad 1.949
## sexoMujer -22.642
## ciuo08Profesionales, científicos e intelectuales -0.242
## ciuo08Técnicos y profesionales de nivel medio -2.068
## ciuo08Personal de apoyo administrativo -2.447
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -12.684
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -16.335
## ciuo08Artesanos y operarios de oficios -14.811
## ciuo08Operadores de instalaciones, maquinas y ensambladores -7.645
## ciuo08Ocupaciones elementales -14.120
## ciuo08Otros no identificados 0.164
## ciuo08Sin clasificación -5.018
## est_conyugalSin pareja -4.234
## Pr(>|z|)
## (Intercept) < 0.0000000000000002
## edad 0.0513
## sexoMujer < 0.0000000000000002
## ciuo08Profesionales, científicos e intelectuales 0.8086
## ciuo08Técnicos y profesionales de nivel medio 0.0386
## ciuo08Personal de apoyo administrativo 0.0144
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados < 0.0000000000000002
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros < 0.0000000000000002
## ciuo08Artesanos y operarios de oficios < 0.0000000000000002
## ciuo08Operadores de instalaciones, maquinas y ensambladores 0.0000000000000209
## ciuo08Ocupaciones elementales < 0.0000000000000002
## ciuo08Otros no identificados 0.8701
## ciuo08Sin clasificación 0.0000005213460582
## est_conyugalSin pareja 0.0000229391302821
##
## (Intercept) ***
## edad .
## sexoMujer ***
## ciuo08Profesionales, científicos e intelectuales
## ciuo08Técnicos y profesionales de nivel medio *
## ciuo08Personal de apoyo administrativo *
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados
## ciuo08Sin clasificación ***
## est_conyugalSin pareja ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 29882 on 26820 degrees of freedom
## Residual deviance: 26541 on 26807 degrees of freedom
## AIC: 26569
##
## Number of Fisher Scoring iterations: 13
e) Incorporando el diseño muestral
No obstante, como se revisó en el práctico anterior, es fundamental utilizar los ponderadores para estimar de forma más precisa, al incorporar el diseño muestral en el modelamiento. En aras de ello, especificamos fact_cal_esi (nuestro ponderador) en el argumento weights =
modelo3_dis <- glm(ing_medio ~ edad + sexo + ciuo08 + est_conyugal,
data = datos,
weights = fact_cal_esi,
family = binomial(link = "logit"))
summary(modelo3_dis)
##
## Call:
## glm(formula = ing_medio ~ edad + sexo + ciuo08 + est_conyugal,
## family = binomial(link = "logit"), data = datos, weights = fact_cal_esi)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -625.3 0.0 0.0 0.0 571.7
##
## Coefficients:
## Estimate
## (Intercept) 734490901694669
## edad 1396302676615
## sexoMujer -977967704379870
## ciuo08Profesionales, científicos e intelectuales -54746519092886
## ciuo08Técnicos y profesionales de nivel medio 696469468409673
## ciuo08Personal de apoyo administrativo 432112479093228
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 1765629792332694
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -364742422184976
## ciuo08Artesanos y operarios de oficios 1343303108100302
## ciuo08Operadores de instalaciones, maquinas y ensambladores -143012874087013
## ciuo08Ocupaciones elementales 975377515779369
## ciuo08Otros no identificados 531401274444271
## ciuo08Sin clasificación 1382778698593716
## est_conyugalSin pareja -79208396226639
## Std. Error
## (Intercept) 152111
## edad 1863
## sexoMujer 51328
## ciuo08Profesionales, científicos e intelectuales 136122
## ciuo08Técnicos y profesionales de nivel medio 139620
## ciuo08Personal de apoyo administrativo 157031
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 133142
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 195056
## ciuo08Artesanos y operarios de oficios 139181
## ciuo08Operadores de instalaciones, maquinas y ensambladores 148683
## ciuo08Ocupaciones elementales 133676
## ciuo08Otros no identificados 369810
## ciuo08Sin clasificación 747979
## est_conyugalSin pareja 58047
## z value
## (Intercept) 4828655221
## edad 749631359
## sexoMujer -19053496735
## ciuo08Profesionales, científicos e intelectuales -402186339
## ciuo08Técnicos y profesionales de nivel medio 4988340807
## ciuo08Personal de apoyo administrativo 2751772874
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 13261260571
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -1869940506
## ciuo08Artesanos y operarios de oficios 9651508941
## ciuo08Operadores de instalaciones, maquinas y ensambladores -961866725
## ciuo08Ocupaciones elementales 7296603904
## ciuo08Otros no identificados 1436959492
## ciuo08Sin clasificación 1848685437
## est_conyugalSin pareja -1364553727
## Pr(>|z|)
## (Intercept) <0.0000000000000002
## edad <0.0000000000000002
## sexoMujer <0.0000000000000002
## ciuo08Profesionales, científicos e intelectuales <0.0000000000000002
## ciuo08Técnicos y profesionales de nivel medio <0.0000000000000002
## ciuo08Personal de apoyo administrativo <0.0000000000000002
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados <0.0000000000000002
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros <0.0000000000000002
## ciuo08Artesanos y operarios de oficios <0.0000000000000002
## ciuo08Operadores de instalaciones, maquinas y ensambladores <0.0000000000000002
## ciuo08Ocupaciones elementales <0.0000000000000002
## ciuo08Otros no identificados <0.0000000000000002
## ciuo08Sin clasificación <0.0000000000000002
## est_conyugalSin pareja <0.0000000000000002
##
## (Intercept) ***
## edad ***
## sexoMujer ***
## ciuo08Profesionales, científicos e intelectuales ***
## ciuo08Técnicos y profesionales de nivel medio ***
## ciuo08Personal de apoyo administrativo ***
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados ***
## ciuo08Sin clasificación ***
## est_conyugalSin pareja ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 8361355 on 26820 degrees of freedom
## Residual deviance: 172389943 on 26807 degrees of freedom
## AIC: 172388965
##
## Number of Fisher Scoring iterations: 25
Sin embargo, como podemos darnos cuenta, el output que generamos incorporando este argumento resulta problemático, y difiere en demasía del modelo que no contempla los ponderadores en su estimación. ¿Qué podemos hacer? ¡pues recurriremos a una librería ya conocida! Nos referimos a srvyr, que nos permitirá crear un objeto encuesta
esi_design <- as_survey_design(datos,
ids = 1,
weights = fact_cal_esi)
¿srvyr también tiene una función para crear modelos de regresión logística? Lamentablemente no. No obstante, y tal como se revisó en el práctico anterior, la librería ``surveyincluye la funciónsvyglm(), que permite estimar modelos de diversas características, considerando el **diseño muestral** de los datos. Esto se especifica con el argumento design =, donde debemos especificar el objeto encuesta con que nos hallamos trabajando (es el símil de data =englm()`).
modelo3_survey <- svyglm(ing_medio ~ edad + sexo + ciuo08 + est_conyugal,
family = binomial(link = "logit"),
design = esi_design)
summary(modelo3_survey)
##
## Call:
## svyglm(formula = ing_medio ~ edad + sexo + ciuo08 + est_conyugal,
## design = esi_design, family = binomial(link = "logit"))
##
## Survey design:
## Called via srvyr
##
## Coefficients:
## Estimate
## (Intercept) 3.299012
## edad 0.003268
## sexoMujer -0.697013
## ciuo08Profesionales, científicos e intelectuales -0.433479
## ciuo08Técnicos y profesionales de nivel medio -0.611823
## ciuo08Personal de apoyo administrativo -0.786611
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -2.191474
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -2.844311
## ciuo08Artesanos y operarios de oficios -2.488899
## ciuo08Operadores de instalaciones, maquinas y ensambladores -1.434649
## ciuo08Ocupaciones elementales -2.226708
## ciuo08Otros no identificados 11.317728
## ciuo08Sin clasificación -2.074388
## est_conyugalSin pareja -0.120082
## Std. Error
## (Intercept) 0.220901
## edad 0.001796
## sexoMujer 0.053237
## ciuo08Profesionales, científicos e intelectuales 0.230493
## ciuo08Técnicos y profesionales de nivel medio 0.225032
## ciuo08Personal de apoyo administrativo 0.244913
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados 0.210180
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros 0.221381
## ciuo08Artesanos y operarios de oficios 0.212019
## ciuo08Operadores de instalaciones, maquinas y ensambladores 0.224929
## ciuo08Ocupaciones elementales 0.208978
## ciuo08Otros no identificados 0.235485
## ciuo08Sin clasificación 0.646857
## est_conyugalSin pareja 0.062022
## t value
## (Intercept) 14.934
## edad 1.820
## sexoMujer -13.093
## ciuo08Profesionales, científicos e intelectuales -1.881
## ciuo08Técnicos y profesionales de nivel medio -2.719
## ciuo08Personal de apoyo administrativo -3.212
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados -10.427
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros -12.848
## ciuo08Artesanos y operarios de oficios -11.739
## ciuo08Operadores de instalaciones, maquinas y ensambladores -6.378
## ciuo08Ocupaciones elementales -10.655
## ciuo08Otros no identificados 48.061
## ciuo08Sin clasificación -3.207
## est_conyugalSin pareja -1.936
## Pr(>|t|)
## (Intercept) < 0.0000000000000002
## edad 0.06883
## sexoMujer < 0.0000000000000002
## ciuo08Profesionales, científicos e intelectuales 0.06003
## ciuo08Técnicos y profesionales de nivel medio 0.00656
## ciuo08Personal de apoyo administrativo 0.00132
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados < 0.0000000000000002
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros < 0.0000000000000002
## ciuo08Artesanos y operarios de oficios < 0.0000000000000002
## ciuo08Operadores de instalaciones, maquinas y ensambladores 0.000000000182
## ciuo08Ocupaciones elementales < 0.0000000000000002
## ciuo08Otros no identificados < 0.0000000000000002
## ciuo08Sin clasificación 0.00134
## est_conyugalSin pareja 0.05287
##
## (Intercept) ***
## edad .
## sexoMujer ***
## ciuo08Profesionales, científicos e intelectuales .
## ciuo08Técnicos y profesionales de nivel medio **
## ciuo08Personal de apoyo administrativo **
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados ***
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros ***
## ciuo08Artesanos y operarios de oficios ***
## ciuo08Operadores de instalaciones, maquinas y ensambladores ***
## ciuo08Ocupaciones elementales ***
## ciuo08Otros no identificados ***
## ciuo08Sin clasificación **
## est_conyugalSin pareja .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1.023958)
##
## Number of Fisher Scoring iterations: 13
5. Extracción de elementos
La extracción de elementos en modelos de regresión logística no difiere de la extracción de elementos de modelos de regresión lineal (ni de cualquier lista).
Coeficientes:
modelo3$coefficients
## (Intercept)
## 3.184303390
## edad
## 0.002146798
## sexoMujer
## -0.756990374
## ciuo08Profesionales, científicos e intelectuales
## -0.040840086
## ciuo08Técnicos y profesionales de nivel medio
## -0.344910420
## ciuo08Personal de apoyo administrativo
## -0.439180226
## ciuo08Trabajadores de los servicios y vendedores de comercios y mercados
## -1.989663484
## ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros
## -2.695957420
## ciuo08Artesanos y operarios de oficios
## -2.346363767
## ciuo08Operadores de instalaciones, maquinas y ensambladores
## -1.273413838
## ciuo08Ocupaciones elementales
## -2.208623846
## ciuo08Otros no identificados
## 11.524043703
## ciuo08Sin clasificación
## -2.460523471
## est_conyugalSin pareja
## -0.167129643
Sexto coeficiente (considerando el intercepto como primero):
modelo3$coefficients[6]
## ciuo08Personal de apoyo administrativo
## -0.4391802
Coeficiente de estado conyugal (sin pareja):
modelo3$coefficients["est_conyugalSin pareja"]
## est_conyugalSin pareja
## -0.1671296
También podemos extraer elementos de los modelos creados con svyglm(); por ejemplo:
Devianza
summary(modelo3_survey)$deviance
## [1] 25003.52
Criterio de Información de Akaike (AIC)
summary(modelo3_survey)$aic
## [1] 23784.76
Podemos utilizar, tal como en el práctico anterior, sjPlot::get_model_data() para extraer los valores predichos
get_model_data(modelo3_survey,
type = "pred")
## $edad
## # Predicted probabilities of ¿Mayor que el ingreso medio?
##
## edad | Predicted | group_col | 95% CI
## -------------------------------------------
## 10 | 0.97 | edad | [0.95, 0.98]
## 20 | 0.97 | edad | [0.95, 0.98]
## 30 | 0.97 | edad | [0.95, 0.98]
## 40 | 0.97 | edad | [0.95, 0.98]
## 60 | 0.97 | edad | [0.96, 0.98]
## 70 | 0.97 | edad | [0.96, 0.98]
## 80 | 0.97 | edad | [0.96, 0.98]
## 100 | 0.97 | edad | [0.96, 0.98]
##
## Adjusted for:
## * sexo = Hombre
## * ciuo08 = Directores, gerentes y administradores
## * est_conyugal = Con pareja
##
## $sexo
## # Predicted probabilities of ¿Mayor que el ingreso medio?
##
## sexo | Predicted | group_col | 95% CI
## -------------------------------------------
## 1 | 0.97 | sexo | [0.95, 0.98]
## 2 | 0.94 | sexo | [0.91, 0.96]
##
## Adjusted for:
## * edad = 42.13
## * ciuo08 = Directores, gerentes y administradores
## * est_conyugal = Con pareja
##
## $ciuo08
## # Predicted probabilities of ¿Mayor que el ingreso medio?
##
## ciuo08 | Predicted | group_col | 95% CI
## ---------------------------------------------
## 1 | 0.97 | ciuo08 | [0.95, 0.98]
## 2 | 0.95 | ciuo08 | [0.94, 0.96]
## 4 | 0.93 | ciuo08 | [0.91, 0.95]
## 5 | 0.78 | ciuo08 | [0.75, 0.80]
## 6 | 0.64 | ciuo08 | [0.60, 0.69]
## 7 | 0.72 | ciuo08 | [0.69, 0.75]
## 8 | 0.88 | ciuo08 | [0.86, 0.90]
## 11 | 0.80 | ciuo08 | [0.54, 0.93]
##
## Adjusted for:
## * edad = 42.13
## * sexo = Hombre
## * est_conyugal = Con pareja
##
## $est_conyugal
## # Predicted probabilities of ¿Mayor que el ingreso medio?
##
## est_conyugal | Predicted | group_col | 95% CI
## ------------------------------------------------------
## 1 | 0.97 | est_conyugal | [0.95, 0.98]
## 2 | 0.96 | est_conyugal | [0.95, 0.98]
##
## Adjusted for:
## * edad = 42.13
## * sexo = Hombre
## * ciuo08 = Directores, gerentes y administradores
Exponenciación de coeficientes
Como bien sabemos, los log-odds son difícilmente interpretables. Para subsanar ello, podemos exponenciar los logaritmos de las chances que figuran en los coeficientes de nuestros modelos de regresión logística, recurriendo a la función exp(). Esto permitirá que nuestro coeficientes pasen de estar en log-odds a Odds-ratio, cuya interpretación es mucho más sencilla. Probemos con el coeficiente para las personas cuyo estatus conyugal es Sin pareja
exp(modelo3_survey$coefficients["est_conyugalSin pareja"])
## est_conyugalSin pareja
## 0.8868479
Luego, podemos crear los OR en nuestro modelo:
modelo3_survey$or <- exp(modelo3_survey$coefficients)
¡Comprobemos!
modelo3_survey$or["est_conyugalSin pareja"]
## est_conyugalSin pareja
## 0.8868479
modelo3_survey$coefficients["est_conyugalSin pareja"]
## est_conyugalSin pareja
## -0.1200818
6. Presentación del modelo creado
a) Tablas
En este práctico revisaremos dos maneras de presentar nuestros modelos. La primera sigue la línea de la práctica anterior, empleando sjPlot::tab_model(). La segunda es algo mas sofisticada: utilizaremos la librería texreg para presentar nuestros modelos, incorporando elementos adicionales a los coeficientes, como lo pueden ser las medidas de ajuste.
Con sjPlot::tab_model()
Seguimos la misma idea del práctico anterior:
sjPlot::tab_model(modelo0,
show.ci=FALSE,
df.method = 'wald', #Para realizar más rápidamente el cálculo de los intervalos de confianza
encoding = "UTF-8")
| ¿Mayor que el ingreso medio? |
||
|---|---|---|
| Predictors | Odds Ratios | p |
| (Intercept) | Inf | <0.001 |
| Observations | 26821 | |
| R2 Tjur | 0.000 | |
Podemos incorporar más de un modelo de regresión a la tabla. Esto es muy útil para comparar los diversos modelos que creamos
sjPlot::tab_model(list(modelo0, modelo1, modelo2), # los modelos estimados
show.ci=FALSE, # no mostrar intervalo de confianza (por defecto lo hace)
p.style = "stars", # asteriscos de significación estadística
df.method = 'wald',
dv.labels = c("Modelo 1", "Modelo 2", "Modelo 3"), # etiquetas de modelos o variables dep.
string.pred = "Predictores", string.est = "β", # nombre predictores y símbolo beta en tabla
encoding = "UTF-8")
| Modelo 1 | Modelo 2 | Modelo 3 | |
|---|---|---|---|
| Predictores | ß | ß | ß |
| (Intercept) | Inf *** | 3.62 *** | 3.85 *** |
| Edad de la persona | 1.00 *** | ||
| Sexo: Mujer | 0.62 *** | ||
| Observations | 26821 | 26821 | 26821 |
| R2 Tjur | 0.000 | 0.001 | 0.011 |
| * p<0.05 ** p<0.01 *** p<0.001 | |||
No obstante, hay algo que resulta un poco problemático: el output de tab_model() cuando presentamos modelos de regresión logística, por defecto, presenta los coeficientes en log-Odds (logaritmo de las chances). Estos valores son difícilmente interpretables. Sin embargo ¡existe una solución! Si especificamos el argumento transform = "exp", el output de la tabla estará en formato Odds ratio (OR), lo cual permite interpretar los coeficientes de manera sencilla.
sjPlot::tab_model(modelo3, # modelo con todas las variables
show.ci=FALSE, # no mostrar intervalo de confianza (por defecto lo hace)
transform = 'exp', # exponenciamos los coeficientes
p.style = "stars", # asteriscos de significación estadística
df.method = 'wald', #Para realizar más rápidamente el cálculo de los intervalos de confianza
dv.labels = "Modelo con todas las variables", # etiquetas de modelos o variables dep.
string.pred = "Predictores", string.est = "β", # nombre predictores y símbolo beta en tabla
encoding = "latin9")
| Modelo con todas las variables | |
|---|---|
| Predictores | ß |
| (Intercept) | 24.15 *** |
| Edad de la persona | 1.00 |
| Sexo: Mujer | 0.47 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Profesionales, cientÃficos e intelectuales |
0.96 |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Técnicos y profesionales de nivel medio |
0.71 * |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Personal de apoyo administrativo |
0.64 * |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Trabajadores de los servicios y vendedores de comercios y mercados |
0.14 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros |
0.07 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Artesanos y operarios de oficios |
0.10 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Operadores de instalaciones, maquinas y ensambladores |
0.28 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Ocupaciones elementales |
0.11 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Otros no identificados |
101118.03 |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Sin clasificación |
0.09 *** |
| est_conyugal: Sin pareja | 0.85 *** |
| Observations | 26821 |
| R2 Tjur | 0.118 |
| * p<0.05 ** p<0.01 *** p<0.001 | |
¡Ahora podemos interpretar los coeficientes de manera sencilla, para cada categoría de respuesta!
¿Y si queremos integrar el diseño muestral?
sjPlot::tab_model(modelo3_survey, # modelo con todas las variables
show.ci=FALSE, # no mostrar intervalo de confianza (por defecto lo hace)
transform = 'exp', # exponenciamos los coeficientes
p.style = "stars", # asteriscos de significación estadística
df.method = 'wald',#Para realizar más rápidamente el cálculo de los intervalos de confianza
dv.labels = "Modelo con todas las variables", # etiquetas de modelos o variables dep.
string.pred = "Predictores", string.est = "β", # nombre predictores y símbolo beta en tabla
encoding = "UTF-8")
| Modelo con todas las variables | |
|---|---|
| Predictores | ß |
| (Intercept) | 27.09 *** |
| Edad de la persona | 1.00 |
| Sexo: Mujer | 0.50 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Profesionales, cientÃficos e intelectuales |
0.65 |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Técnicos y profesionales de nivel medio |
0.54 ** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Personal de apoyo administrativo |
0.46 ** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Trabajadores de los servicios y vendedores de comercios y mercados |
0.11 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros |
0.06 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Artesanos y operarios de oficios |
0.08 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Operadores de instalaciones, maquinas y ensambladores |
0.24 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Ocupaciones elementales |
0.11 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Otros no identificados |
82267.21 *** |
| b1. Grupo ocupacional según CIUO 08 - 1 dÃgito: Sin clasificación |
0.13 ** |
| est_conyugal: Sin pareja | 0.89 |
| Observations | 26821 |
| R2 / R2 adjusted | 0.102 / 0.101 |
| * p<0.05 ** p<0.01 *** p<0.001 | |
Con texreg
La segunda forma de presentar nuestro modelo de en formato tabla es con texreg. Hay diversas funciones:
screenreg(): muestra la tabla en la consola de R.htmlreg(): produce una tabla en formato html. Es la que utilizaremos en este práctico.texreg(): produce una tabla en formato LaTex para documentos en PDF.
Si no especificamos ningún argumento, htmlreg() presenta de forma directa una tabla publicable, con sus respectivas medidas de ajuste. Algo fundamental es especificar results='asis' en las opciones del chunk pues, de lo contrario, la tabla no aparecerá en el documento renderizado.
htmlreg(modelo3, doctype = F)
| Model 1 | |
|---|---|
| (Intercept) | 3.18*** |
| (0.17) | |
| edad | 0.00 |
| (0.00) | |
| sexoMujer | -0.76*** |
| (0.03) | |
| ciuo08Profesionales, científicos e intelectuales | -0.04 |
| (0.17) | |
| ciuo08Técnicos y profesionales de nivel medio | -0.34* |
| (0.17) | |
| ciuo08Personal de apoyo administrativo | -0.44* |
| (0.18) | |
| ciuo08Trabajadores de los servicios y vendedores de comercios y mercados | -1.99*** |
| (0.16) | |
| ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros | -2.70*** |
| (0.17) | |
| ciuo08Artesanos y operarios de oficios | -2.35*** |
| (0.16) | |
| ciuo08Operadores de instalaciones, maquinas y ensambladores | -1.27*** |
| (0.17) | |
| ciuo08Ocupaciones elementales | -2.21*** |
| (0.16) | |
| ciuo08Otros no identificados | 11.52 |
| (70.48) | |
| ciuo08Sin clasificación | -2.46*** |
| (0.49) | |
| est_conyugalSin pareja | -0.17*** |
| (0.04) | |
| AIC | 26569.19 |
| BIC | 26683.95 |
| Log Likelihood | -13270.60 |
| Deviance | 26541.19 |
| Num. obs. | 26821 |
| ***p < 0.001; **p < 0.01; *p < 0.05 | |
¡Podemos incluir más de un modelo!
htmlreg(l = list(modelo3, modelo3_survey))
| Model 1 | Model 2 | |
|---|---|---|
| (Intercept) | 3.18*** | 3.30*** |
| (0.17) | (0.22) | |
| edad | 0.00 | 0.00 |
| (0.00) | (0.00) | |
| sexoMujer | -0.76*** | -0.70*** |
| (0.03) | (0.05) | |
| ciuo08Profesionales, científicos e intelectuales | -0.04 | -0.43 |
| (0.17) | (0.23) | |
| ciuo08Técnicos y profesionales de nivel medio | -0.34* | -0.61** |
| (0.17) | (0.23) | |
| ciuo08Personal de apoyo administrativo | -0.44* | -0.79** |
| (0.18) | (0.24) | |
| ciuo08Trabajadores de los servicios y vendedores de comercios y mercados | -1.99*** | -2.19*** |
| (0.16) | (0.21) | |
| ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros | -2.70*** | -2.84*** |
| (0.17) | (0.22) | |
| ciuo08Artesanos y operarios de oficios | -2.35*** | -2.49*** |
| (0.16) | (0.21) | |
| ciuo08Operadores de instalaciones, maquinas y ensambladores | -1.27*** | -1.43*** |
| (0.17) | (0.22) | |
| ciuo08Ocupaciones elementales | -2.21*** | -2.23*** |
| (0.16) | (0.21) | |
| ciuo08Otros no identificados | 11.52 | 11.32*** |
| (70.48) | (0.24) | |
| ciuo08Sin clasificación | -2.46*** | -2.07** |
| (0.49) | (0.65) | |
| est_conyugalSin pareja | -0.17*** | -0.12 |
| (0.04) | (0.06) | |
| AIC | 26569.19 | |
| BIC | 26683.95 | |
| Log Likelihood | -13270.60 | |
| Deviance | 26541.19 | 25003.52 |
| Num. obs. | 26821 | 26821 |
| Dispersion | 1.02 | |
| ***p < 0.001; **p < 0.01; *p < 0.05 | ||
A diferencia de tab_model(), htmlreg() arroja, por defecto, los coeficientes en log-odds. Podemos realizar la transformación a OR de la siguiente manera, recurriendo a la función extract() de texreg
or <- texreg::extract(modelo3_survey) #Extraemos info del modelo
or@coef <- exp(or@coef) #Exponenciamos los coeficientes
Y ahora construimos la tabla
htmlreg(l = list(modelo3_survey, or))
| Model 1 | Model 2 | |
|---|---|---|
| (Intercept) | 3.30*** | 27.09*** |
| (0.22) | (0.22) | |
| edad | 0.00 | 1.00 |
| (0.00) | (0.00) | |
| sexoMujer | -0.70*** | 0.50*** |
| (0.05) | (0.05) | |
| ciuo08Profesionales, científicos e intelectuales | -0.43 | 0.65 |
| (0.23) | (0.23) | |
| ciuo08Técnicos y profesionales de nivel medio | -0.61** | 0.54** |
| (0.23) | (0.23) | |
| ciuo08Personal de apoyo administrativo | -0.79** | 0.46** |
| (0.24) | (0.24) | |
| ciuo08Trabajadores de los servicios y vendedores de comercios y mercados | -2.19*** | 0.11*** |
| (0.21) | (0.21) | |
| ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros | -2.84*** | 0.06*** |
| (0.22) | (0.22) | |
| ciuo08Artesanos y operarios de oficios | -2.49*** | 0.08*** |
| (0.21) | (0.21) | |
| ciuo08Operadores de instalaciones, maquinas y ensambladores | -1.43*** | 0.24*** |
| (0.22) | (0.22) | |
| ciuo08Ocupaciones elementales | -2.23*** | 0.11*** |
| (0.21) | (0.21) | |
| ciuo08Otros no identificados | 11.32*** | 82267.21*** |
| (0.24) | (0.24) | |
| ciuo08Sin clasificación | -2.07** | 0.13** |
| (0.65) | (0.65) | |
| est_conyugalSin pareja | -0.12 | 0.89 |
| (0.06) | (0.06) | |
| Deviance | 25003.52 | 25003.52 |
| Dispersion | 1.02 | 1.02 |
| Num. obs. | 26821 | 26821 |
| ***p < 0.001; **p < 0.01; *p < 0.05 | ||
¡Personalicemos la tabla! Hay diversos argumentos (especificados a continuación) que permiten incorporar diversos elementos a la tabla, como pueden ser los intervalos de confianza para cada uno de los coeficientes, titular cada uno de los modelos presentados, agregar notas al pie de la tabla, entre otros. Si les interesa profundizar en la personalización de estas tablas, pueden dirigirse a la documentación de la función.
htmlreg(l = list(modelo3_survey, or),
doctype = F, #No incluimos doctype
caption = "Leyenda", #Leyenda de la tabla
caption.above = T, # Presentar la leyenda en la sección superior. Si = FALSE (predeterminado), la leyenda se sitúa bajo la tabla
custom.model.names = c("Modelo 3", "Modelo 3 (OR)"), #Personalizar los títulos de la tabla
ci.force = c(TRUE,TRUE), #Presentar intervalos de confianza
override.coef = list(coef(modelo3_survey), or@coef), #Sobreescribir los coeficientes a partir de los coeficientes de los modelos
custom.note = "$^{***}$ p < 0.001; $^{**}$ p < 0.01; $^{*}$ p < 0.05 <br> Errores estándar entre paréntesis. <br> **Nota**: La significancia estadística de los coeficientes en unidades de Odds ratio está calculada en base a los valores $t$, <br> los cuales a su vez se calculan en base a $log(Odds)/SE$") #Incorporamos una nota al pie de la tabla
| Modelo 3 | Modelo 3 (OR) | |
|---|---|---|
| (Intercept) | 3.30* | 27.09* |
| [ 2.87; 3.73] | [ 26.65; 27.52] | |
| edad | 0.00 | 1.00* |
| [-0.00; 0.01] | [ 1.00; 1.01] | |
| sexoMujer | -0.70* | 0.50* |
| [-0.80; -0.59] | [ 0.39; 0.60] | |
| ciuo08Profesionales, científicos e intelectuales | -0.43 | 0.65* |
| [-0.89; 0.02] | [ 0.20; 1.10] | |
| ciuo08Técnicos y profesionales de nivel medio | -0.61* | 0.54* |
| [-1.05; -0.17] | [ 0.10; 0.98] | |
| ciuo08Personal de apoyo administrativo | -0.79* | 0.46 |
| [-1.27; -0.31] | [ -0.02; 0.94] | |
| ciuo08Trabajadores de los servicios y vendedores de comercios y mercados | -2.19* | 0.11 |
| [-2.60; -1.78] | [ -0.30; 0.52] | |
| ciuo08Agricultores y trabajadores calificados agropecuarios, forestales y pesqueros | -2.84* | 0.06 |
| [-3.28; -2.41] | [ -0.38; 0.49] | |
| ciuo08Artesanos y operarios de oficios | -2.49* | 0.08 |
| [-2.90; -2.07] | [ -0.33; 0.50] | |
| ciuo08Operadores de instalaciones, maquinas y ensambladores | -1.43* | 0.24 |
| [-1.88; -0.99] | [ -0.20; 0.68] | |
| ciuo08Ocupaciones elementales | -2.23* | 0.11 |
| [-2.64; -1.82] | [ -0.30; 0.52] | |
| ciuo08Otros no identificados | 11.32* | 82267.21* |
| [10.86; 11.78] | [82266.75; 82267.67] | |
| ciuo08Sin clasificación | -2.07* | 0.13 |
| [-3.34; -0.81] | [ -1.14; 1.39] | |
| est_conyugalSin pareja | -0.12 | 0.89* |
| [-0.24; 0.00] | [ 0.77; 1.01] | |
| Deviance | 25003.52 | 25003.52 |
| Dispersion | 1.02 | 1.02 |
| Num. obs. | 26821 | 26821 |
| $^{***}$ p < 0.001; `\(^{**}\)` p < 0.01; `\(^{*}\)` p < 0.05 Errores estándar entre paréntesis. **Nota**: La significancia estadística de los coeficientes en unidades de Odds ratio está calculada en base a los valores `\(t\)`, los cuales a su vez se calculan en base a `\(log(Odds)/SE\)` |
||
b) Gráficos
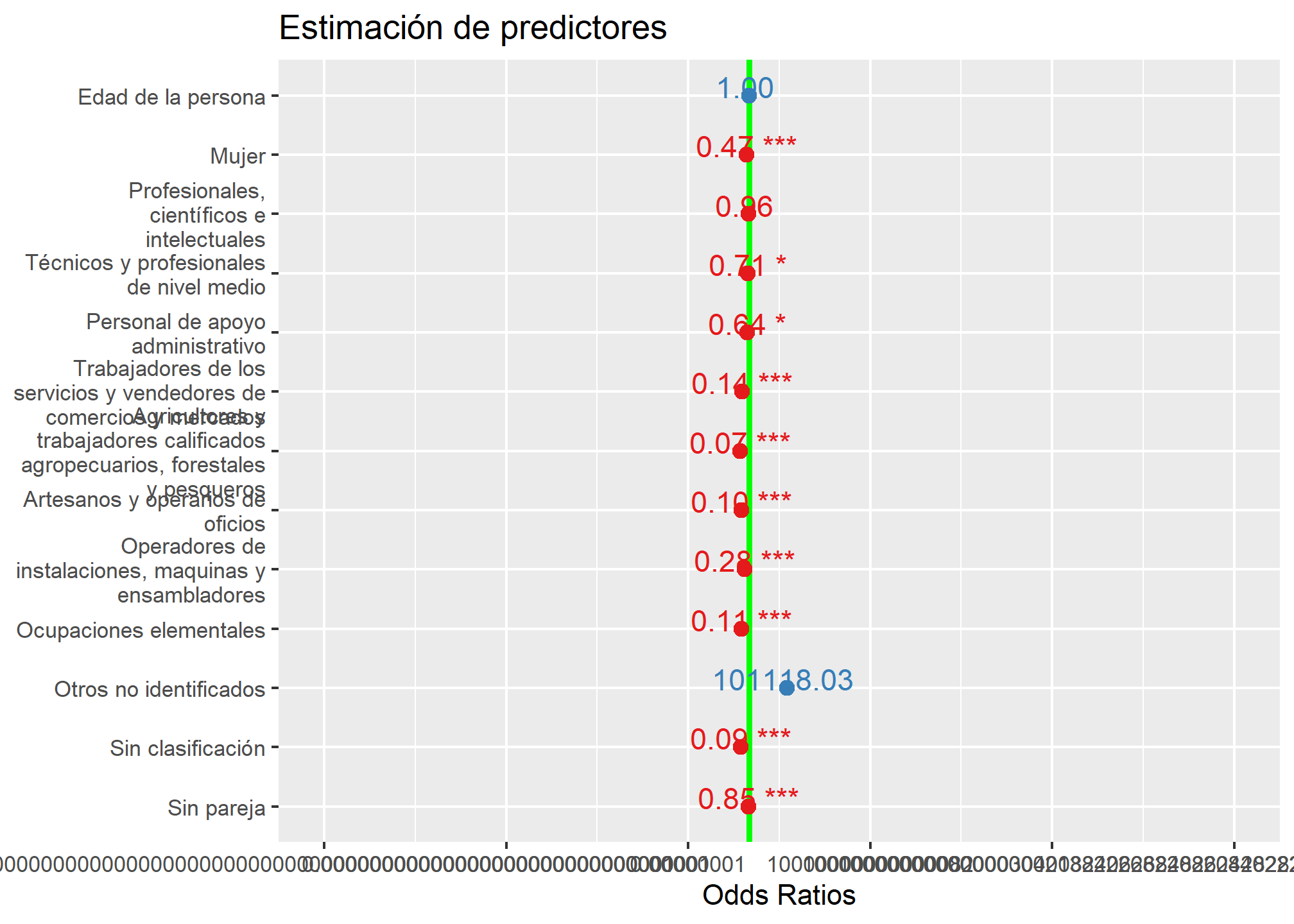
(Una vez más) tal como en el práctico anterior, utilizaremos la librería sjPlot para graficar nuestros modelos. En particular, su función plot_model() nos permitirá presentar los modelos de manera gráfica. Esta vez, no obstante, el output por defecto es en Odds ratio. `
sjPlot::plot_model(modelo3,
show.p = T,
show.values = T,
ci.lvl = 0.95,
title = "Estimación de predictores",
vline.color = "green")
7. Resumen
En este práctico aprendimos a
- Crear modelos de regresión logística binomial
- Calcular tales modelos incorporando el diseño muestral
- Representar gráficamente los modelos con tablas y gráficos
- Personalizar tales tablas y gráficos